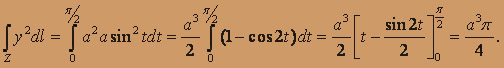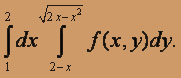
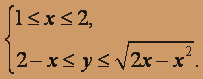
Главная страница О курсе Введение Программа по курсу математики для студентов второго курса заочного факультета Литература Задания для контрольных работ Методические указания к выполнению контрольных работ			Кратные и криволинейные интегралы Задание 1. Изменить порядок интегрирования. Сделать чертёж: Решение. Изобразим область интегрирования, для чего выпишем пределы изменения x и y: Уравнение 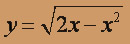– это верхняя полуокружность, r =1 и центр в точке(1;0). Второе уравнение – это прямая, проходящая через точки (2,0) и (0,2). Заданная область заштрихована на чертеже. 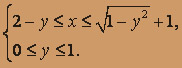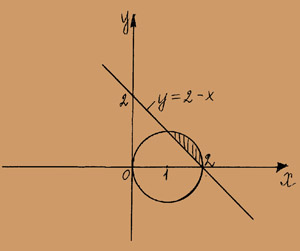Для этой области имеем: Следовательно, данный интеграл, поменяв порядок интегрирования, можно записать так: Задание 2. 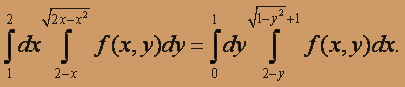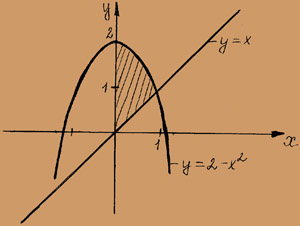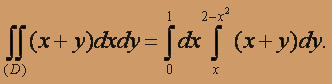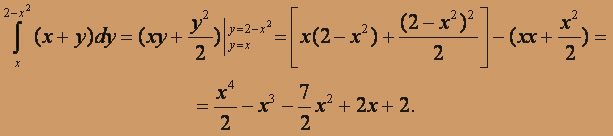Вычислить двойной интеграл (x+ y)dx dy по области (D), ограниченной линиями: x = 0, x =1, y =x, y =2 - x2 Решение: Область D ограничена прямыми x = 0, y = x и параболой y = 2 - x2, тогда Вычисляем внутренний интеграл, считая x постоянным: Вычисляем внешний интеграл: 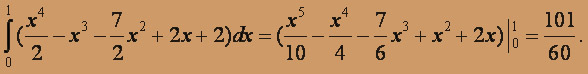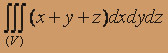Задание 3. Вычислить тройной интеграл по области V, заданной поверхностями x + y + z =1, x = 0, y = 0, z = 0. Решение. Изобразим область V на чертеже. Это пирамида, ограниченная плоскостью x + y + z =1 и координатными плоскостями x=0, y = 0, z = 0. Область V проецируется на плоскость Oxy в треугольник, ограниченный прямыми x = 0, y = 0, y = 1 - x. 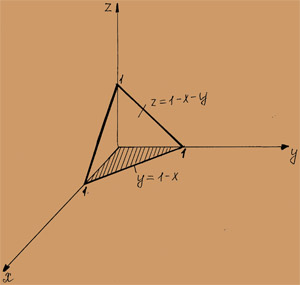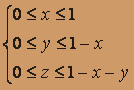Опишем область интегрирования с помощью неравенств V: Вычислим интеграл: Задание 4. Вычислить объём тела, ограниченного поверхностями x + y + z = 3, z = 2, x = 0, y = 0. 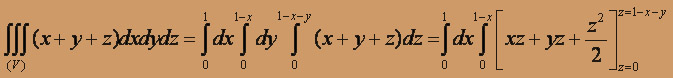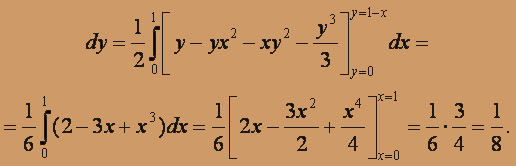Решение. V = 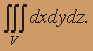Тело снизу ограничено плоскостью z = 2, сверху - плоскостью x + y + z = 3, поэтому предел интегрирования по z определяется неравенством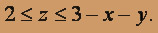 V = 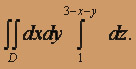На плоскость XOY тело проецируется в треугольник D, ограниченный прямыми x = 0, y = 0, x + y = 1.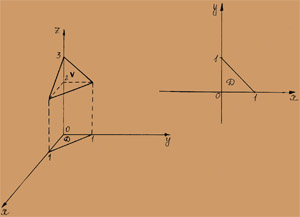 "Нижней" границей области D является ось OX, т. е. прямая y=0. "Верхней" границей - прямая y = 1 - x. 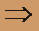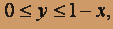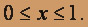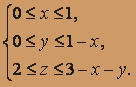Пределы интегрирования по y определяются неравенством а по x: Итак, D: Следовательно, Задание 5. 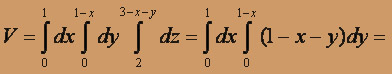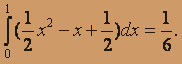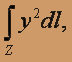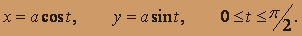Вычислить криволинейный интеграл I рода: где Z - часть окружности Решение. Так как то дифференциал дуги 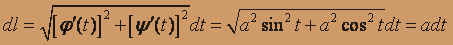Следовательно, получаем: