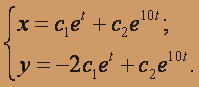О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
Приводим к виду уравнения с разделяющимися переменными
x2y2 (dy / dx) = y - 1
x2y2 dy = (y - 1) dx | 1 / (x2(y - 1))
Разделяем переменные:
(y2 / (y - 1)) dy = dx / x2
Переменные разделены. Интегрируем обе части уравнения:
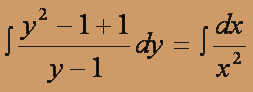
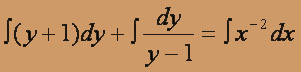
y2 / 2 + y + ln(y - 1) = - 1 / x + c - это есть общий интеграл д. у.
Используя начальное условие y(0) = 1 , подставляем в выражение общего интеграла заданные значения переменных x = 0, y = 1 - тем самым определяем значение с (произвольной постоянной):
1 / 2 + 1 + ln 0 = c
откуда с=2,5.
Итак, искомый частный интеграл имеет вид y2 / 2 + y + ln(y - 1) = - 1 / x + 2,5
(x2 + y2)dx - xydy = 0.
Здесь M(x, y)= (x2+y2), N(x, y) =-ху
M(Kx, Ky)=(K2x2+ K2y2)= K2(x2+y2), N(Kx, Ky)=(-KxKy)= K2(-xy). Данное уравнение является однородным, так как M(x,y),N(x,y) – однородные функции второго измерения.
Разрешим уравнение относительно производной dy / dx:
y' = (x2 + y2) / xy
Поделив числитель и знаменатель правой части уравнения на х2, получим
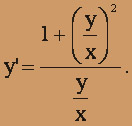
t=y/x, y=tx, y' = t'x + t (dy=tdx+xdt).
Уравнение (1) преобразуется в уравнение с разделяющимися переменными
t'x + t = (1 + t2) / t, или x dt / dx = 1/ t, откуда dx / x = t dt
Интегрируя это уравнение, получим
ln | x | = t2 / 2 + ln c, откуда ln (x / c) = t2 / 2, т.е. x = cet2/2
Заменяя в последнем равенстве t отношением y / x окончательно получим: x = cey2/ (2 x2) .
1-й способ (метод вариаций произвольных постоянных)
Записываем соответствующее однородное линейное уравнение:
Уравнение с разделяющимися переменными (разделяем переменные)
dy = (y / x) dx,
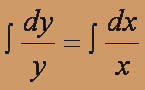, y = c1x.Ищем решение неоднородного уравнения в виде:
y = c1(x)x.
где с1(х) – неизвестная функция переменной х.
Подставляя в уравнение (2) y = c1(x)x и y' = c'1(x)x + c1(x) , имеем:
Уравнение с разделяющимися переменными (разделяем переменные)
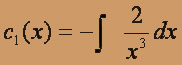, c'1(x) = 1 / x2 + c2.Таким образом, общее решение неоднородного уравнения имеет вид:
2-ой способ (метод Бернулли)
Ищем решение уравнения в виде
v(u' - (1/x) u) + uv' = - 2 / x2; (4)
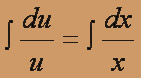, u (x) = xc1v' x = - 2/ x2, v' = - 2/ x3. v = 1 / x2 + c2.
Таким образом, общее решение уравнения имеет вид:
y'' = x + cos x (y'' = f(x) - уравнение не содержит y,y').
Интегрируя, получим:
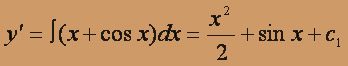
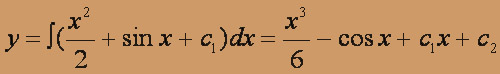
где с1,с2 – произвольные постоянные.
y''(x2 + 1) = 2xy' (y'' = f(x, y') - уравнение не содержит y).
Замена y' = p = p(x), y'' = p' dp / dx и данное уравнение принимает вид
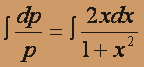
ln p = ln (x2 + 1) + ln c1; p = c1(x2 + 1).
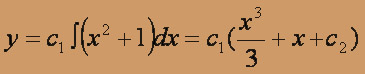
yy'' = y'2 (y'' = f(y, y') - уравнение не содержит x).
Замена y' = p = p(y), y'' = p dp / dy
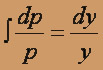
ln p = ln y + ln c1; p = yc1.
y'' - 2 y' + 5y = 0. Составим характеристическое уравнение k2 - 2 k + 5 = 0, из которого находим корни
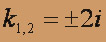(комплексные 
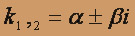), при этом 
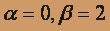Следовательно, общее решение уравнения имеет вид: Составим характеристическое уравнение
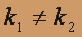)Составим общее решение уравнения
Составим характеристическое уравнение
Составим общее решение уравнения
Найдем общее решение
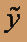соответствующего однородного уравненияРешая отвечающее ему характеристическое уравнение
получаем корни k1= 1, k2= -4 Следовательно,
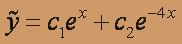
Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть f(x) = (x + 1)ex имеет вид
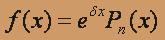: n=1,P1(x)=x+1 
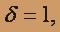причем 
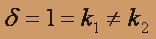. Следовательно, частное решение у* нужно искать в виде: y* = (Ax + B)xex = (Ax2 + Bx)ex
,где А, В – некоторые коэффициенты, подлежащие определению. Для их отыскания найдем у*’ и у*’’:
(y*)'' = 2Aex + (2A + B)ex + (2Ax + B)ex + (Ax2 + Bx)ex
2Aex + (2A + B)ex + (2Ax + B)ex + (Ax2 + Bx)ex + 3
(2Ax + B)ex + 3 (Ax2 + Bx)ex.
-4 (Ax2 + Bx)ex = (x + 1)ex
xex : 2A + B + 6A + 3B - 4B = 1
ex : 2A + 2A + B + B + 3B = 1
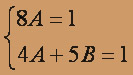
Решая эту систему, найдем A = 1/8, B = 1/10 . Таким образом, получаем искомое частное решение
Теперь можно записать общее решение данного уравнения
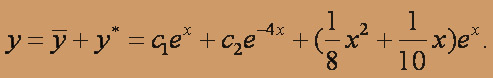
Найдем общее решение
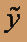соответствующего однородного уравненияРешая отвечающее ему характеристическое уравнение
получаем корни
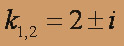Следовательно, 
Ищем у*. Здесь правая часть f(x) = 2cosx + 6sinx имеет вид
: a=2,b=6,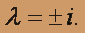 
. Числа 
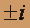не являются корнями характеристического уравнения, поэтому частное решение у* нужно искать в виде где А, В – неопределенные коэффициенты.
Найдем производные у*' и у*'':
y*'' = - A cos x - B sin x.
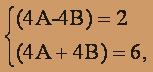
откуда А=1, В= 1/2 . Таким образом y* = cos x + (1/2) sin x
Итак, общее решение данного уравнения имеет вид
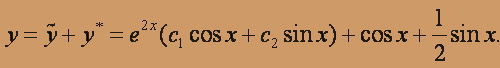
Записываем соответствующее однородное уравнение:
k2 + 1 = 0
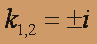
Применяем метод Лагранжа (метод вариации произвольных постоянных):
Ищем решение данного уравнения в виде
Записываем систему уравнений для определения ф. C'1(x) и C'2(x):
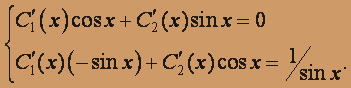
Решая её, получим
C'1(x) = -1; C'2(x) = ctg x
Интегрируя, находим
C1(x) = -x; C2(x) = ln (sin x)
Записываем полученное общее решение данного неоднородного решения
Характеристическое уравнение k2- 5k + 4 = 0; имеет корни k1= 1, k2= 4 . Общее решение соответствующего однородного уравнения:
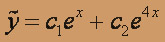
Здесь правая часть f(x) = cos x - 3sin x, т.е.
, 
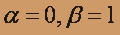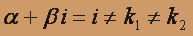, i - не является корнем характеристического уравнения, поэтому частное решение у* неоднородного уравнения нужно искать в виде:Приравняем коэффициенты при подобных членах
sin x : - B + 5A + 4B = - 3
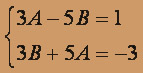
A = - 6 / 17, B = - 7 / 17.
Общее решение неоднородного уравнения
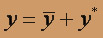
Искомое решение
y' = c1ex + 4c2e4x + (6 / 17) sin x - (7 / 17) cos x.
Используем начальные условия
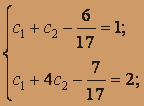, c1 = 1, c2 = 6 / 17Искомое частное решение
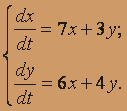
Характеристическое уравнение имеет вид
k2 - 11k + 10 = 0; k1 = 1, k2 = 10,
Для корня k1 = 1 составляем систему линейных уравнений
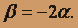
Полагая
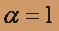, находим 
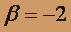и записываем первое частное решение системы.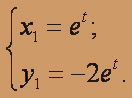 
Система уравнений для корня k2 = 10 имеет вид
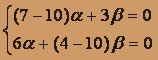
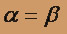
Полагая
, 
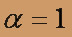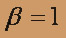, получим второе частное решение
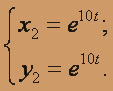
Общее решение системы имеет вид:
