Главная страница О курсе Введение Программа по курсу математики для студентов второго курса заочного факультета Литература Задания для контрольных работ Методические указания к выполнению контрольных работ	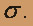		VII. Векторный анализ Задание 1.Даны векторное поле F=Xi+Y j+Zk и плоскость Ax + By + Cz +D = O(p) которая совместно с координатными плоскостями образует пирамиду V. Пусть - основание пирамиды, принадлежащее плоскости (p); 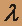- контур, ограничивающий 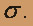; n – нормаль к 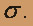, направленная вне пирамиды V. Требуется вычислить. 1)поток векторного поля F через поверхность 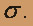в направлении нормали n; 2)циркуляцию векторного поля F по замкнутому контуру 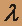непосредственно и применив теорему Стокса к контуру 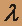и ограниченной им поверхности 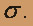с нормалью n; 3)поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности непосредственно и применив теорему Остроградского. Сделать чертеж. F = (x + z) i; x + y + z - 2 = 0. F = (y – x + z) j; 2x - y + 2z - 2 = 0. F = (x +7z) k; 2x + y + z - 4 = 0. F = (x + 2y – z) i; - x + 2y + 2z - 4 = 0. F = (2x + 3y – 3z) j; 2x - 3y + 2z - 6 = 0. F = (2x + 4y + 3z) k; 3x + 2y + 3z - 6 = 0. F = (x – y + z) i; - x + 2y + z - 4 = 0. F = (3x + 4y + 2z) j; x + y + 2z - 4 = 0. F = (5x + 2y + 3z) k; x + y + 3z - 3 = 0. F = (x – 3y + 6z) i; - x + y + 2z - 4 = 0. Задание 2. Проверить, является ли векторное поле F =Xi + Yj + Zk потенциальным и соленоидальным. В случае потенциальности поля F найти его потенциал. F = (6x + 7yz) i + (6y + 7xz) j + (6z + 7xy) k. F = (8x – 5yz) i + (8y – 5xz) j + (8z – 5xy) k. F = (10x – 3yz) i + (10y – 3xz) j + (10z – 3xy) k. F = (12x + yz) i + (12y + xz) j + (12z + xy) k. F = (4x – 7yz) i + (4y – 7xz) j + (4z – 7xy) k. F = (x + 2yz) i + (y + 2xz) j + (z + 2xy) k. F = (5x + 4yz) i + (5y + 4xz) j + (5z + 4xy) k. F = (7x – 2yz) i + (7y – 2xz) j + (7z – 2xy) k. F = (3x – yz) i + (3y – xz) j + (3z – xy) k. F = (9x + 5yz) i + (9y + 5xz) j + (9z + 5xy) k.