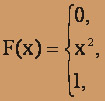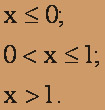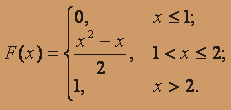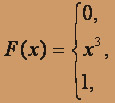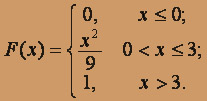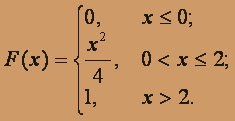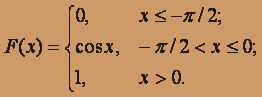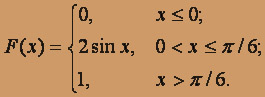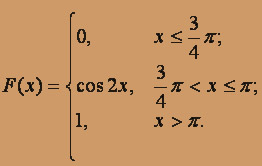Главная страница

О курсе

Введение

Программа по курсу математики для студентов второго курса заочного факультета

Литература

Задания для контрольных работ

Методические указания к выполнению контрольных работ



VI. Теория вероятностей и элементы математической статистики




Задание 1.В партии из 10 деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей k стандартных.
  1. n=8, m=5, k=4;
  2. n=5, m=7, k=4;
  3. n=7, m=7, k=5;
  4. n=5, m=8, k=3;
  5. n=9, m=5, k=4;
  6. n=6, m=7, k=5.
  7. n=7, m=3, k=2.
  8. n=4, m=8, k=2.
  9. n=5, m=3, k=1.
  10. n=6, m=9, k=5


Задание 2. На полке расставлены в произвольном порядке n книг. Определить вероятность того, что k определенных книг окажутся поставленными рядом.
  1. n=15, k=3;
  2. n=12, k=3;
  3. n=12, k=4;
  4. n=10, k=2;
  5. n=10, k=5;
  6. n=11, k=3.
  7. n=8, k=2.
  8. n=9, k=4.
  9. n=9, k=7.
  10. n=11, k=5.


Задание 3. Моменты начала двух событий наудачу распределены в промежутке времени от T1 до T2. Одно из событий длится 10 минут, другое-t минут. Определить вероятность того, что:
а) события «перекрываются» по времени;
б) «не перекрываются».
  1. T1 = 9.00, T2 = 10.00, t = 10;
  2. T1 = 10.00, T2 = 10.30, t = 15;
  3. T1 = 18.00, T2 = 19.00, t = 10;
  4. T1 = 15.00, T2 = 16.30, t = 20;
  5. T1 = 17.00, T2 = 18.00, t = 15;
  6. T1 = 9.00, T2 = 11.00, t = 20;
  7. T1 = 12.00, T2 = 13.00, t = 5;
  8. T1 = 16.00, T2 = 17.30, t = 5;
  9. T1 = 15.00, T2 = 15.30, t = 12;
  10. T1 = 20.00, T2 = 21.30, t = 12;


Задание 4. Два станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки, равна p1 , а второй - p2 . Найти вероятность того, что:
а) оба станка проработают смену без наладки;
б) только один станок проработает смену без наладки;
в) оба станка за смену потребуют наладки;
г) хотя бы один станок за смену потребует наладки.
  1. p1 = 0.9, p2 = 0.8;
  2. p1 = 0.9, p2 = 0.7;
  3. p1 = 0.8, p2 = 0.75;
  4. p1 = 0.6, p2 = 0.9;
  5. p1 = 0.6, p2 = 0.75;
  6. p1 = 0.8, p2 = 0.7;
  7. p1 = 0.85, p2 = 0.65;
  8. p1 = 0.75, p2 = 0.9;
  9. p1 = 0.8, p2 = 0.8;
  10. p1 = 0.65, p2 = 0.9;


Задание 5. В первой урне N1 белых и M1 черных шаров, во второй N2 белых и M 2 черных. Из первой во вторую переложено K шаров, затем из второй урны извлечен один шар. Определить вероятность того, что выбранный из второй урны шар – белый.
  1. N1 = 4, M1 = 1, N2 = 2, M2 = 5, K = 3;
  2. N1 = 7, M1 = 3, N2 = 5, M2 = 1, K = 4;
  3. N1 = 2, M1 = 3, N2 = 5, M2 = 4, K = 1;
  4. N1 = 8, M1 = 2, N2 = 3, M2 = 2, K = 5;
  5. N1 = 6, M1 = 4, N2 = 1, M2 = 7, K = 2;
  6. N1 = 3, M1 = 2, N2 = 4, M2 = 4, K = 2;
  7. N1 = 5, M1 = 2, N2 = 6, M2 = 3, K = 3;
  8. N1 = 3, M1 = 5, N2 = 7, M2 = 1, K = 2;
  9. N1 = 4, M1 = 2, N2 = 3, M2 = 2, K = 2;
  10. N1 = 5, M1 = 4, N2 = 2, M2 = 5, K = 4;


Задание 6. В магазин поступают однотипные изделия с трех заводов, причем i-й завод поставляет mi% изделий ( i =1,2,3 ). Среди изделий i-го завода ni% первосортных. Куплено одно изделие, оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено j-м заводом.
  1. m1 = 50%, m2 = 20%, n1 = 70%, n2 = 80%, n3 =90 % , j=1;
  2. m1 = 20%, m2 = 20%, n1 = 80%, n2 = 80%, n3 = 90% , j=2;
  3. m1 = 60%, m2 = 20%, n1 = 90%, n2 = 90%, n3 = 80% , j=3;
  4. m1 = 40%, m2 = 30%, n1 = 80%, n2 = 90%, n3 = 80% , j=1;
  5. m1 = 40%, m2 = 20%, n1 = 90%, n2 = 80%, n3 = 90% , j=2;
  6. m1 = 40%, m2 = 30%, n1 = 70%, n2 = 70%, n3 = 80% , j=3;
  7. m1 = 30%, m2 = 50%, n1 = 60%, n2 = 70%, n3 = 80% , j=1;
  8. m1 = 30%, m2 = 40%, n1 = 90%, n2 = 60%, n3 = 70% , j=2;
  9. m1 = 70%, m2 = 10%, n1 = 80%, n2 = 70%, n3 = 70% , j=3;
  10. m1 = 40%, m2 = 30%, n1 = 60%, n2 = 80%, n3 = 80% , j=1.


Задание 7. Вероятность выигрыша в лотерею на один билет равна p. Куплено n билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.
  1. p = 0.3, n = 10;
  2. p = 0.5, n = 11;
  3. p = 0.7, n = 11;
  4. p = 0.2, n = 10;
  5. p = 0.5, n = 10;
  6. p = 0.4, n = 12;
  7. p = 0.6, n = 10;
  8. p = 0.3, n = 15;
  9. p = 0.3, n = 12;
  10. p = 0.2, n = 12;


Задание 8. Вероятность того, что деталь не прошла проверку ОТК, равна p. Найти вероятность того, что среди n случайно отобранных деталей окажутся непроверенными от k1 до k2 деталей.
  1. n = 600, k1 = 400, k2 = 450, p = 0.5;
  2. n = 500, k1 = 250, k2 = 300, p = 0.4;
  3. n = 400, k1 = 200, k2 = 250, p = 0.6;
  4. n = 300, k1 = 150, k2 = 165, p = 0.5;
  5. n = 350, k1 = 150, k2 = 200, p = 0.4;
  6. n = 100, k1 = 60, k2 = 75, p = 0.6;
  7. n = 700, k1 = 550, k2 = 600, p = 0.5;
  8. n = 200, k1 = 100, k2 = 450, p = 0.5;
  9. n = 450, k1 = 250, k2 = 300, p = 0.8;
  10. n = 300, k1 = 100, k2 = 200, p = 0.6.


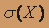Задание 9. Найти математическое ожидание М(Х), дисперсию D(X), среднее квадратическое отклонение , функцию распределения вероятностей F(X) (и начертить ее) дискретной случайной величины Х, заданной законом распределения:
X
x1
x2
x3
x4
P
p1
p2
p3
p4

(k равно номеру Вашего варианта).
x1 = 3k
x2 = 5k
x3 = 7k
x4 = 9k
p1 = 0.1
p2 = 0.2
p3 = 0.4
p4 = 0.1



Задание 10. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.


Задание 11. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю х объемом выборки n и среднее квадратичное отклонение
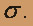
  1. x = 75,17; n = 36; 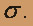= 6;
  2. x = 75,16; n = 49; 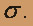= 7;
  3. x = 75,15; n = 64; 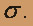= 8;
  4. x = 75,14; n = 81; 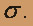= 9;
  5. x = 75,13; n = 100; 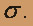= 10;
  6. x = 75,12; n = 121; 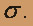= 11;
  7. x = 75,11; n = 144; 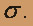= 12;
  8. x = 75,10; n = 169; 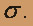= 13;
  9. x = 75,09; n = 196; 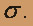= 14;
  10. x = 75,08; n = 22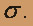5; = 15;