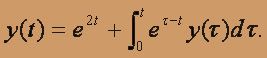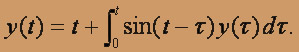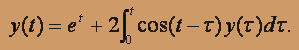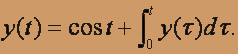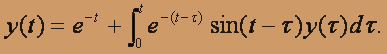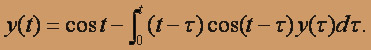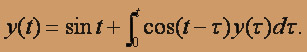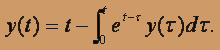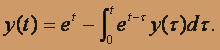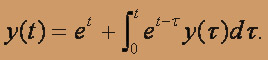О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
- а) f(t) = e3tcos 3t cos 4t, б) f(t) = t sin t sh2t,
- а) f(t) = e-4tsin 3t cos 2t, б) f(t) = t e-2tsin t,
- а) f(t) = tcos 3t cos t, б) f(t) = t sh t sin 2t,
- а) f(t) = sin3t, б) f(t) = t2 sin 2t,
- а) f(t) = sh t cos t sin 3t, б) f(t) = te- t cos t,
- а) f(t) = ch 2t cos 2t, б) f(t) = t cos23t. 2,
- а) f(t) = t sin 2t sin 3t, б) f(t) = (sh 2t) / t,
- а) f(t) = ch t sin 2t sin t, б) f(t) = (e2tsin t) / t,
- а) f(t) = ch 2t sin 2t , б) f(t) = (sh 2t + sh t) / t,
- а) f(t) = t ch 3t cos t, б) f(t) = t sh2t.
- а)
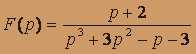 ; б)
; б)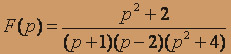 .
.
- а)
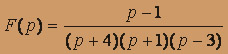 ; б)
; б)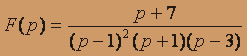 .
.
- а)
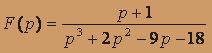 ; б)
; б)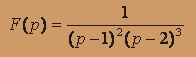 .
.
- а)
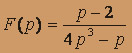 ; б)
; б)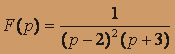 .
.
- а)
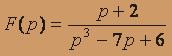 ; б)
; б)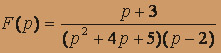 .
.
- а)
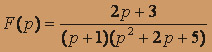 ; б)
; б)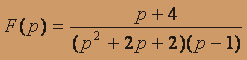 .
.
- а)
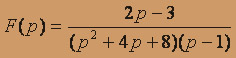 ; б)
; б)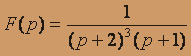 .
.
- а)
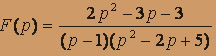 ; б)
; б)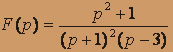 .
.
- а)
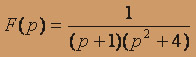 ; б)
; б)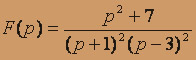 .
.
- а)
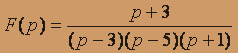 ; б)
; б)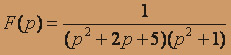 .
.
- F(p) = p2 / ( p2 + 1)2;
- F(p) = p / ( p2 + 4);
- F(p) = 3 / (p2( p2 + 9));
- F(p) = p2 / (( p2 + 1)( p2 + 4));
- F(p) = p / (( p2 + 1)( p + 1));
- F(p) = 3 / p ( p2 + 25);
- F(p) = 1 / (( p2 + 4)( p - 2));
- F(p) = 1 / ( p2 + 1)2;
- F(p) = p / (( p2 + 1)( p2 + 9));
- F(p) = 1 / (p2( p2 + 1));
- x''' + x'' = sin t ; x(0) = 1; x'(0) = 1; x''(0) = 0.
- x'' - x' = tet; x(0) = 0; x'(0) = 1.
- x''' - 2x'' + x' = 4; x(0) = 1; x'(0) = 2; x''(0) = -2.
- x'' - 9x = e- 2t; x(0) = 0; x'(0) = 0.
- x'' + x' = t2 + 2t; x(0) = 4; x'(0) = - 2.
- x'' + 9x = cos 3t; x(0) = 1; x'(0) = 0.
- x''' + x = 1; x(0) = 0; x'(0) = 0; x''(0) = 0.
- x'' - 4x = t - 1; x(0) = 0; x'(0) = 0.
- x'' + 2x' + x = cos t; x(0) = 0; x'(0) = 0.
- x'' + 3x' + 2x = 1 + t + t2; x(0) = 0; x'(0) = 1.
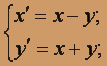 ; x(0) = 1; y (0) = 0.
; x(0) = 1; y (0) = 0.
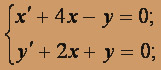 ; x(0) = 2; y (0) = 3.
; x(0) = 2; y (0) = 3.
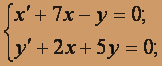 ; x(0) = 1; y (0) = 1.
; x(0) = 1; y (0) = 1.
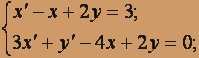 ; x(0) = 0; y (0) = 0.
; x(0) = 0; y (0) = 0.
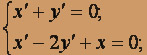 ; x(0) = 1; y (0) = - 1.
; x(0) = 1; y (0) = - 1.
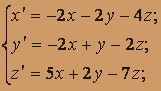 ; x(0) = 1; y (0) = 0; z (0) = 1.
; x(0) = 1; y (0) = 0; z (0) = 1.
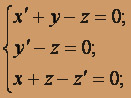 ; x(0) = 2; y (0) = 1/2; z (0) = 5/2.
; x(0) = 2; y (0) = 1/2; z (0) = 5/2.
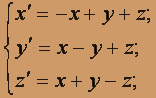 ; x(0) = 2; y (0) = 2; z (0) = - 1.
; x(0) = 2; y (0) = 2; z (0) = - 1.
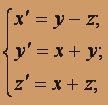 ; x(0) = 1; y (0) = 2; z (0) = 3.
; x(0) = 1; y (0) = 2; z (0) = 3.
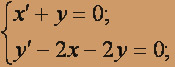 ; x(0) = 1; y (0) = 1.
; x(0) = 1; y (0) = 1.