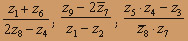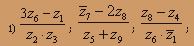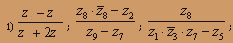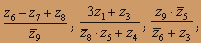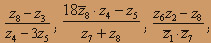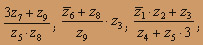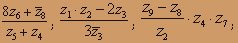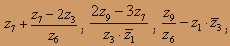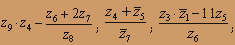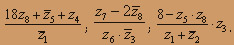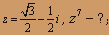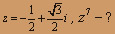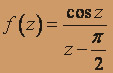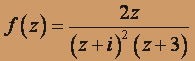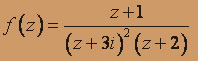О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
- z4 + 4z2 + 3 = 0;
- z4 - 6iz2 - 8 = 0;
- z6 - 5z3 + 6 = 0;
- z8 - z4 - 8 = 0;
- z4 - 6z2 + 45 = 0;
- z6 + 4z3 + 3 = 0;
- z4 + iz2 + 2 = 0;
- z6 + 2z3 - 15 = 0;
- z4 - 3z2 - 4 = 0;
- z4 - 3iz2 - 2 = 0;
- W = ez + 1 / z, z0 = 2 + i ;
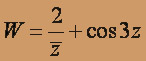 , z0 = 1 - i ;
, z0 = 1 - i ;
- W = ln z + z3,
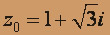 ;
;
- W = sin 2z + cos z + z2, z0 = 2 - i ;
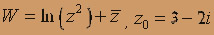 ;
;
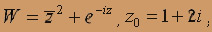 ;
;
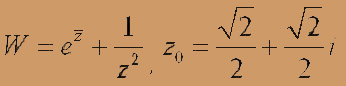 ;
;
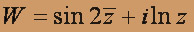 , z0 = 2 + 3i;
, z0 = 2 + 3i;
- W = sh( z + i) + z3,
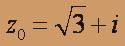 ;
;
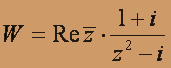 , z0 = 1 + i.
, z0 = 1 + i.
- f (z) = cos (iz);
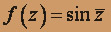 ;
;
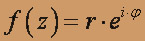 ;
;
- f (z) = ch z;
- f (z) = z ez;
- f (z) = z Rez;
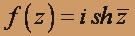 ;
;
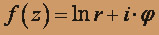 , где z = r eik
, где z = r eik
- f (z) = e3z;
- f (z) = iz2 - 3z + 1.
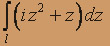 ,где l - отрезок прямой от точки z0 = i до точки z1 = 1;
,где l - отрезок прямой от точки z0 = i до точки z1 = 1;
 ,где l - дуга параболы y = 2x2 от точки z0 = 0 до точки z1 = 1 +2i;
,где l - дуга параболы y = 2x2 от точки z0 = 0 до точки z1 = 1 +2i;
 ,где l - дуга окружности |z| = 3 от точки z0 = 3 до точки z1 = 3e2
,где l - дуга окружности |z| = 3 от точки z0 = 3 до точки z1 = 3e2 i;
i;
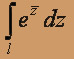 ,где l отрезок прямой от точки z0 = i до точки z1 =
,где l отрезок прямой от точки z0 = i до точки z1 =  +
+  i;
i;
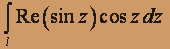 ,где l отрезок прямой от точки z0 = (1/2)(
,где l отрезок прямой от точки z0 = (1/2)( - i) до точки z1 = (1/2)(
- i) до точки z1 = (1/2)( + i);
+ i);
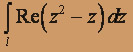 ,где l дуга параболы y =2x2 от точки z0 = 0 до точки z1 = 1 + 2i;
,где l дуга параболы y =2x2 от точки z0 = 0 до точки z1 = 1 + 2i;
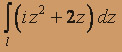 ,где l отрезок прямой от точки z0 = 0 до точки z1 = 1 + i;
,где l отрезок прямой от точки z0 = 0 до точки z1 = 1 + i;
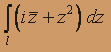 , где l - часть окружности |z| = 2
, где l - часть окружности |z| = 2 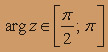 ;
;
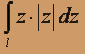 ,где l дуга окружности |z| = 1 от точки z0 = 1 до точки z1 = e2
,где l дуга окружности |z| = 1 от точки z0 = 1 до точки z1 = e2 i;
i;
 ,где l отрезок прямой от точки z0 = 0 до точки z1 =
,где l отрезок прямой от точки z0 = 0 до точки z1 =  -
-  i;
i;
- f(z) = 1 / (z - 3) + 3 / (z - 6), z0 = 4; D : 1 < |z - 4| < 2;
- f(z) = 1 / (z + 2) +1 / (z + 5), z0 = - 3; D : 1 < |z + 3| < 2;
- f(z) = 1 / (z + i) - 3 / (z + 4i), z0 = - 2i; D : 1 < |z + 2i| < 2;
- f(z) = 1 / (z + 2i) + 1 / (z + 6i), z0 = - 3i; D : 1 < |z + 3i| < 2;
- f(z) = 2i / (z + 3) + 3 / (z + 6), z0 = - 4; D : 1 < |z + 4| < 2;
- f(z) = 1 / (z - i) + 2i / (z - 4i), z0 = 2i; D : 1 < |z - 2i| < 2;
- f(z) = i / (z + 2) + 2 / (z + 7), z0 = - 4; D : 1 < |z + 4| < 3;
- f(z) = 3i / (z - i) + 2 / (z - 5i), z0 = 2i; D : 1 < |z - 2i| < 3;
- f(z) = 3 / (z + 4) + i / (z + 8), z0 = - 5; D : 1 < |z + 5| < 3;
- f(z) = i / (z - 1) + 2 / (z - 8), z0 = 4; D : 3 < |z - 4| < 4;