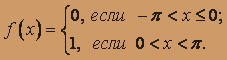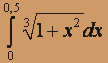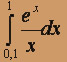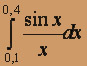О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
- а)
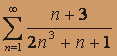 ; б)
; б) 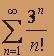 ; в)
; в) 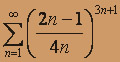 .
.
- а)
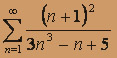 ; б)
; б) 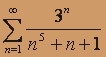 ; в)
; в) 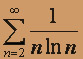 .
.
- а)
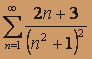 ; б)
; б) 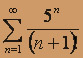 ; в)
; в) 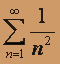 .
.
- а)
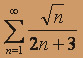 ; б)
; б) 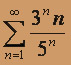 ; в)
; в) 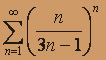 .
.
- а)
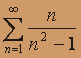 ; б)
; б) 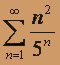 ; в)
; в) 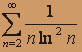 .
.
- а)
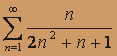 ; б)
; б) 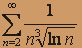 ; в)
; в) 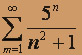 .
.
- а)
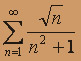 ; б)
; б) 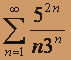 ; в)
; в) 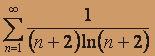 .
.
- а)
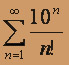 ; б)
; б) 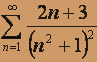 ; в)
; в) 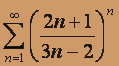 .
.
- а)
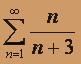 ; б)
; б) 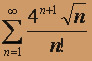 ; в)
; в) 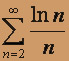 .
.
- а)
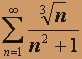 ; б)
; б) 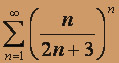 ; в)
; в) 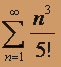 .
.
- а)
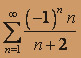 ; б)
; б) 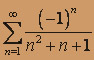 .
.
- а)
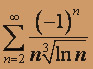 ; б)
; б) 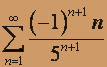 .
.
- а)
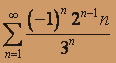 ; б)
; б) 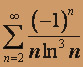 .
.
- а)
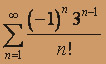 ; б)
; б) 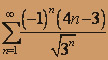 .
.
- а)
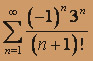 ; б)
; б) 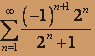 .
.
- а)
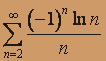 ; б)
; б) 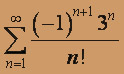 .
.
- а)
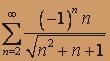 ; б)
; б) 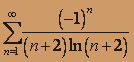 .
.
- а)
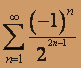 ; б)
; б) 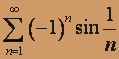 .
.
- а)
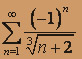 ; б)
; б) 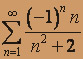 .
.
- а)
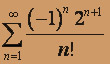 ; б)
; б) 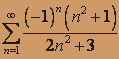 .
.
- а)
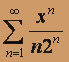 ; б)
; б) 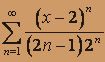 .
.
- а)
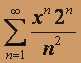 ; б)
; б) 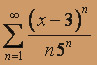 .
.
- а)
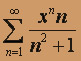 ; б)
; б) 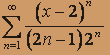 .
.
- а)
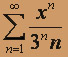 ; б)
; б) 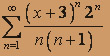 .
.
- а)
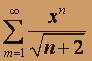 ; б)
; б) 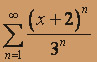 .
.
- а)
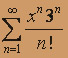 ; б)
; б) 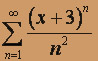 .
.
- а)
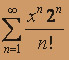 ; б)
; б) 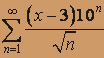 .
.
- а)
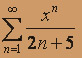 ; б)
; б) 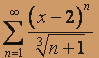 .
.
- а)
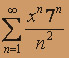 ; б)
; б) 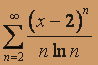 .
.
- а)
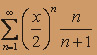 ; б)
; б) 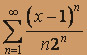 .
.
- а) f(x) = x2e-x ; б) f(x) = cos (x / 2).
- а) f(x) = (sin x) / x; б) f(x) = ex2.
- а) f(x) = (arctg 3x) / x; б)
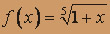 .
.
- а) f(x) = (cos x - 1) / x; б) f(x) = xe- 2x.
- а) f(x) = x- 2 arctg x2; б)
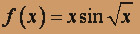 .
.
- а)
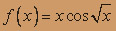 ; б)
; б) 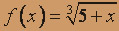 .
.
- а) f(x) = xe- 2x; б) f(x) = ln (1 + x / 2).
- а)
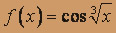 ; б) f(x) = arctg x2.
; б) f(x) = arctg x2.
- а) f(x) = (sin x) / x ; б)
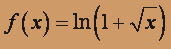 .
.
-
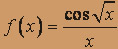 ; б)
; б)  .
.
- f (x) = x + 2, (- 2; 2).
- f (x) = cos (x / 2), ( -
 ;
;  ).
).
- f (x) = e- x, ( -
 ;
;  ).
).
- f (x) = e2x, ( -
 ;
;  ).
).
- f (x) = x2 / 2, (- 3; 3).
- f (x) = x2, ( -
 ;
;  ).
).
- f (x) = 3 - x / 2, (- 3; 3).
- f (x) = sin (x / 2), ( -
 ;
;  ).
).
- f (x) = (2 / 3) x2, (- 3; 3).