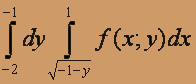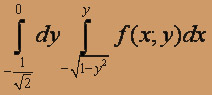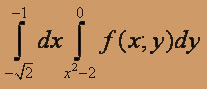О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
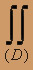 (xy - 3x5y2)dxdy, D: y = - x2, y = | x |, x = 1.
(xy - 3x5y2)dxdy, D: y = - x2, y = | x |, x = 1.
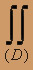 (5x2y + x3y3)dxdy, D: y = - x2/2, y = x.
(5x2y + x3y3)dxdy, D: y = - x2/2, y = x.
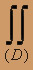 3yexy/4dxdy, D : y = e, y = ln 5, x = 4, x = 8.
3yexy/4dxdy, D : y = e, y = ln 5, x = 4, x = 8.
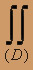 (3x4y2 - 10xy)dxdy, D : y = x2, y = - x.
(3x4y2 - 10xy)dxdy, D : y = x2, y = - x.
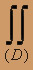 y sin(2xy)dxdy, D : y =
y sin(2xy)dxdy, D : y =  /2 , y = 3/2
/2 , y = 3/2 , x = 1/2, x = 2.
, x = 1/2, x = 2.
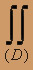 y2e- xydxdy, D : x = 0, y = 1, y = x/2.
y2e- xydxdy, D : x = 0, y = 1, y = x/2.
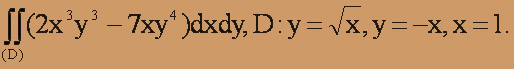
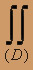 (4xy + x4y5)dxdy, D : y = x2, y = - | x |, x = - 1.
(4xy + x4y5)dxdy, D : y = x2, y = - | x |, x = - 1.
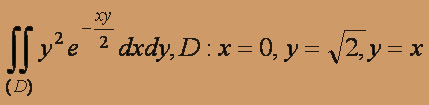
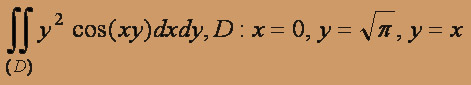
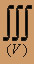 2y2exydxdydz, где V: x = 0, y = 1, y = x, z = 0, z = 1.
2y2exydxdydz, где V: x = 0, y = 1, y = x, z = 0, z = 1.
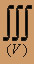 3(y2 + z)dxdydz, где V: x = 0, y = 0, z = 0, x + y = 1, z = x + y.
3(y2 + z)dxdydz, где V: x = 0, y = 0, z = 0, x + y = 1, z = x + y.
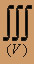 y2z cos(xyz)dxdydz, где V: x = 1, y = 2x, y = 0, z = 0, z = 36.
y2z cos(xyz)dxdydz, где V: x = 1, y = 2x, y = 0, z = 0, z = 36.
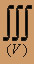 (x + y - z)dxdydz, где V: x = - 1, x = 1, y = 0, y = 1, z = 0, z = 2.
(x + y - z)dxdydz, где V: x = - 1, x = 1, y = 0, y = 1, z = 0, z = 2.
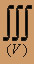 y2exy/2dxdydz, где V: x = 0, y = 2, y = 2x, z = 0, z = - 1.
y2exy/2dxdydz, где V: x = 0, y = 2, y = 2x, z = 0, z = - 1.
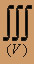 (5x + 6z)dxdydz, где V: x = 0, y = 0, z = 0, x + y + z = 1.
(5x + 6z)dxdydz, где V: x = 0, y = 0, z = 0, x + y + z = 1.
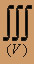 2y2zexyzdxdydz, где V: x = 1, y = 1, z = 1, x = 0, y = 0, z = 0.
2y2zexyzdxdydz, где V: x = 1, y = 1, z = 1, x = 0, y = 0, z = 0.
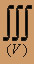 (x2+4y2)dxdydz, где V: z = 2x + y, x + y = 1, x = 0, y = 0, z = 0.
(x2+4y2)dxdydz, где V: z = 2x + y, x + y = 1, x = 0, y = 0, z = 0.
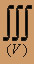 7xzdxdydz, где V: y = x, y = 0, x = 2, z = xy, z = 0.
7xzdxdydz, где V: y = x, y = 0, x = 2, z = xy, z = 0.
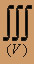 x2 sin ((
x2 sin (( xy)/2)dxdydz, где V: x = 2, y = x, y = 0, z = 0, z =
xy)/2)dxdydz, где V: x = 2, y = x, y = 0, z = 0, z =  .
.
- x2 - 6x + y2 = 0; y = x /
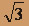 ;
;
x2 - 10x + y2 = 0; y =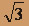 x.
x.
- y2 - 2y + x2 = 0; y = x /
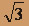 ;
;
y2 - 10y + x2 = 0; x = 0. - x2 - 4x + y2 = 0; y = 0;
x2 - 8x + y2 = 0; y =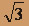 x.
x.
- y2 - 4y + x2 = 0; y = x;
y2 - 2y + x2 = 0; x = 0. - x2 - 2x + y2 = 0; y = 0;
x2 - 6x + y2 = 0; y = x. - (x2 + y2)2 = 2(x2 - y2), x2 + y2 = 1, (вне круга)
- (x2 + y2)2 = 4xy, x2 + y2 =
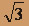 , (вне круга)
, (вне круга)
- (x2 + y2)2 = 3(x2 - y2), x2 + y2 = 3, (вне лемнискаты)
- (x2 + y2)2 = 4(x2 - y2), x2 + y2 = 2, (вне круга)
- (x2 + y2)2 = 8xy, x2 + y2 = 4, (вне лемнискаты).
- z = 0, y = 0, x = 0, x + y = 1, z = x2 + y2.
- z = 0, y = 0, z = 4 - x - y, y = 0, x2 + y2= 4.
- z = 0, y + z = 2, x2 + y2= 4.
- z = 0, x2 + y2 = z, x2 + y2= 4.
- z = x2 + y2, y = x2, y = 1, z = 0.
- z = 0, z = 9 - x2, x2 + y2= 9.
- z = 0, z = y2, x2 + y2= 9.
- z = 0, x = 0, y = 0, x + y + z = 1.
- z = 0, x = 0, y = 0, x + y = 1, z = 2 - x - y.
- z = 0, z = 4
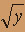 , x = 0, x + y = 4.
, x = 0, x + y = 4.
- x2 + y2 + z2 = 4, z
 0.
0.
- x2 + y2 = 2z, z = 1.
- x2 + y2 + z2 = 2, x2 + y2 = z2, z
 0.
0.
- z = 1 - x2 - y2, z = 0.
- z = 1 + x2 + y2, z = 5.
- z =
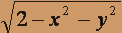 , z = x2 + y2.
, z = x2 + y2.
- z = 8 - x2 - y2, z = -1.
- z2 = x2 + y2, z =
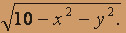
- x2 + y2 + z2 = 1, z (x2 + y2)/2, z
 0.
0.
- x2 + y2 + z2 = 25, z
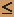 0.
0.
 (x - y)dl, где Z - отрезок прямой между точками А(0;0) и B(0;0).
(x - y)dl, где Z - отрезок прямой между точками А(0;0) и B(0;0).
 dl / (x2 + y2 + z2), где Z – дуга первого витка кривой
dl / (x2 + y2 + z2), где Z – дуга первого витка кривой 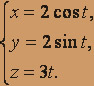
 y / x dl, где Z – дуга параболы y = x2/2 от точки A(1;1/2) до точки B(2;2).
y / x dl, где Z – дуга параболы y = x2/2 от точки A(1;1/2) до точки B(2;2).
 xy dl, где Z – четверть окружности
xy dl, где Z – четверть окружности 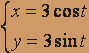 , лежащая в первой четверти.
, лежащая в первой четверти.
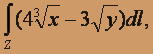 где Z – отрезок прямой между точками A(-1;0) и B(0;1).
где Z – отрезок прямой между точками A(-1;0) и B(0;1).
 (x2 + y2 + z2)dl, где Z – дуга винтовой линии
(x2 + y2 + z2)dl, где Z – дуга винтовой линии 
 y dl, где Z – дуга параболы y2 = 2x от точки О (0;0) до точки А(4;
y dl, где Z – дуга параболы y2 = 2x от точки О (0;0) до точки А(4;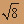 ).
).
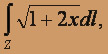 где Z – дуга линии
где Z – дуга линии 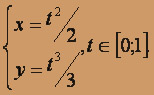
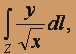 где Z – дуга линии y2 = 4x от точки А (1;2) до точки В(4;4).
где Z – дуга линии y2 = 4x от точки А (1;2) до точки В(4;4).
 x dl, где Z – дуга линии
x dl, где Z – дуга линии 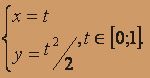
- F = - y
 + x
+ x 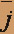 ; Z : y = x3, M(0;0), N(2;8).
; Z : y = x3, M(0;0), N(2;8).
- F = (x + y)
 + (x - y)
+ (x - y)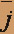 ; Z : x2 + (y2) / 9 = 1, (x
; Z : x2 + (y2) / 9 = 1, (x  0, y
0, y  0, ) M(1;0), N(0;3).
0, ) M(1;0), N(0;3).
- F = (x2 + 2y)
 + (y2 + 2x)
+ (y2 + 2x)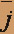 ; Z : y = 2 - x2 / 8, M(- 4;0), N(0;2).
; Z : y = 2 - x2 / 8, M(- 4;0), N(0;2).
- F = 2x
 - (x + 2y)
- (x + 2y)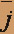 ; где Z – отрезок прямой MN, M(-1;0), N(1;2).
; где Z – отрезок прямой MN, M(-1;0), N(1;2).
- F = xy
 ; Z : y = sin x, M(
; Z : y = sin x, M( ;0), N(0;0).
;0), N(0;0).
- F = (x2 - 2y)
 + (y2 - 2x)
+ (y2 - 2x)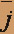 ; где Z – отрезок прямой MN, M(-4;0), N(0;2).
; где Z – отрезок прямой MN, M(-4;0), N(0;2).
- F = (x + y)
 + (x - y)
+ (x - y)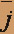 ; Z : y = x2, M(-1;1), N(1;1).
; Z : y = x2, M(-1;1), N(1;1).
- F = x3
 - y3
- y3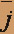 ; Z : x2 + y2 = 4, (x
; Z : x2 + y2 = 4, (x  0, y
0, y  0, ) M(2;0), N(0;2).
0, ) M(2;0), N(0;2).
- F = x2y
 - y
- y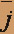 ; где Z – отрезок прямой MN, M(-1;0), N(0;1).
; где Z – отрезок прямой MN, M(-1;0), N(0;1).
- F = (xy - x)
 + (x2 / 2)
+ (x2 / 2)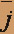 ; Z : x2 / 9 + y2 / 4 = 1, (y
; Z : x2 / 9 + y2 / 4 = 1, (y  0), M(3;0), N(- 3;0).
0), M(3;0), N(- 3;0).