О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
- 2x2yy'+y2=2, y(0)=-2.
- 6xdx-6ydy=2x2ydy-3xy2dx, y(-1)=2.
- y'=tgtgy, y(0) =
 /2
/2
- yy'=(1-2x)/y, y(1)=1.
- (xy2)dx+(y-x2y)dy=0, y(2)= - 2.
- y'cosx - (y + 1) sinx=0, y(
 /3)=1.
/3)=1.
- ln(cosy)dx+xtgydy=0, y(1)=0.
- (x2 - 1)y'+2xy2=0, y(0)=1.
- ((x + 2) / x) dx + ((y-1)/y)dy=0, y(1)=1.
- y' = 3x - y, y(1)=1.
- ydy - xdy = 2x3tg (y/x)dx
- y' = (x - y)/(x - 2y)
- y' =(y/x)+sin (y/x)
- (x - y)dx + (x + y)dy = 0
- xy' - y = x / arctg(y/x)
- y' = (xy2 - yx2)/x3
- (2x2 - 6xy)dy = (x2 + 2xy - 5y2)dx
- xy' = y - xey/x
- y' = (y2 / x2)dy + 4(y/x)+ 2
- (y2 - x2)dy + 2xy dx = 0
- (sin2y + xctgy)y' = 1
- (3x - y2)y' = y
- (x + y2)dy = ydx
- xy' - 2y = 2x4
- y' - ((3y)/x) = 3x
- (xy + ex)dx - xdy = 0
- x2y' + xy + 1
- (xy' - 1)ln x = 2y
- xy' - ytgx = sin x
- y = x (y' - x cos x)
- y'' - (y '/x ) = x2
- y'' - y' ctg x = 2x sin x
- 2 yy'' = y'2 + 1
- y'' tg y = 2( y')2
- xy'' = y' ln (y' / x)
- y'' - 3 (y'/x) = x
- y'' y3 - 1 = 0
- y'' = 2x + sin 4x - 3
- y'' = y' - x2
- y'' = 1/(1 + x2) + x - sin x
- y'' - 7y' = 5xex
- y'' - 9y' = e3x cos x
- y'' + y' = x sinx
- y'' - 2y' +2y =2x
- y'' - 2y' -3y = e4x
- y'' + y = 4sinx
- y'' + 2y' + y = e-xcos x
- y'' + 6y' + 9y = (x - 2)e-3x
- y'' - 3y' + 2y = 10 e - x
- y'' - y = x2-x +1
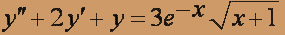
- y'' + 3 y' + 2y = 1/(ex + 1)
- y'' - 6 y' + 9y = e3x/ x
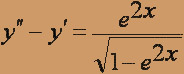
- y'' + 4y = 1/cos 2 x
- y'' + 4y' + 4y = (e-2x/x3)
- y'' + 4y = 2 tgx
- y'' - y' = ex/ (1 + ex)
- y'' + y = 1/ cos x
- y'' - 2y' + y = ex/x
- y'' - y' - 6y = 12x, y'(0) = - 2; y(0)=1;
- y'' - 2y' -3y = 4xex, y'(0) = - 1; y(0)=2;
- y'' + y = 2 cos x, y'(0) = - 1; y(0)=1;
- y'' - 2y' + y = 8e3x, y'(0) = 6; y(0)=3;
- y'' - 3y' = x + cos x, y(0) = 0; y'(0)= -1/9;
- y'' - 2y' = 2ex, y(1) = - 1; y'(1)= 0;
- y'' - 4y' + 8y = e2x + sin 2x, y(0) = 1.35; y'(0)= 1;
- y'' + 2y' + y =(x + 3)e - x, y(0) = 1; y'(0)= 4;
- y'' - 2y' +10y = 10x2 + 18x + 6, y(0) = 1; y'(0)= 3.2;
- y'' - 2y' - 8y = 3x - 4e2x; y(0) = 4; y'(0)=2;
1.
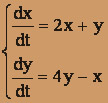 2.
2. 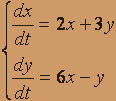 3.
3. 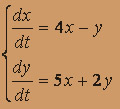 4.
4. 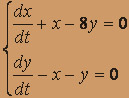 5.
5. 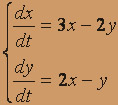 6.
6. 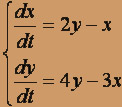 7.
7. 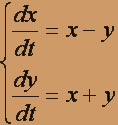 8.
8. 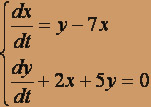 9.
9. 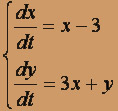 10.
10.