Лекция 7. Понятие линейного преобразования.
Собственные векторы.
Пусть переменные х1 и х2 связаны с переменными х1/ и х2/ следующими формулами
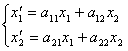 , (1)
, (1)
тогда матрица А =  называется матрицей линейного преобразования вектора
называется матрицей линейного преобразования вектора
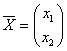 в вектор
в вектор 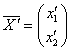 , или точки М(x1, x2) в базисе
, или точки М(x1, x2) в базисе ![]() , в точку М’(x’1, x’2) в базисе
, в точку М’(x’1, x’2) в базисе ![]() .
.
Матричная запись линейного преобразования
![]() .
.
В общем случае ![]() отличаются по величине и по направлению. Важное значение имеют те векторы
отличаются по величине и по направлению. Важное значение имеют те векторы ![]() , которые при линейном преобразовании не меняют прямой, на которой они находились до преобразования.
, которые при линейном преобразовании не меняют прямой, на которой они находились до преобразования.
Определение. Ненулевой вектор ē называется собственным вектором линейного преобразования с матрицей А, если он переводится этой матрицей в вектор, коллинеарный вектору ē, то есть,
Аē = λē, (2)
где λ- некоторое число, которое называется собственным значением матрицы А.
Пусть вектор ē {m;n}, тогда из матричного уравнения (2) следует
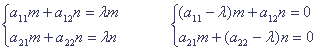 (3)
(3)
Вопрос о существовании собственных векторов сводится к вопросу о существовании ненулевого решения линейной относительно m и n, однородной системы (3).
Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю:
![]()
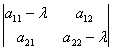 =0 (4)
=0 (4)
Уравнение (4) называется характеристическим уравнением.
В матричном виде уравнение (4):
| A – λ E | = 0. (5)
Уравнение (4) может не иметь действительных корней, и тогда собственных векторов с вещественными координатами нет.
Если корни характеристического уравнения вещественные равные, то можно указать собственный вектор.
Если характеристическое уравнение имеет два различных вещественных корня, то можно найти два собственных вектора.
Симметрическое линейное преобразование.
Линейное преобразование называется симметрическим, если его матрица А симметрична:
А = Ат
Для матрицы размера (2 × 2) это условие имеет вид а12 = а21.
Теорема. Собственные значения симметрического линейного преобразования вещественны, а собственные векторы ортогональны.
Теорема о приведении матрицы к диагональному виду.
Пусть матрица линейного преобразования
А =  .
.
Пусть l1,l2-собственные значения матрицы А, ē1 {m1, n1} и ē2{m2, n2} соответствующие собственные векторы, причем не коллинеарные.
Рассмотрим матрицу из координат собственных векторов:
В=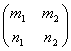 , det(B)¹0, тогда матрица B-1AB=
, det(B)¹0, тогда матрица B-1AB=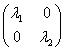 .
.
Преобразование координат при переходе к новому базису
(изменение направления осей).
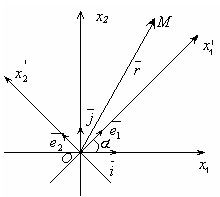
Пусть система координат х10х2 определяется ортонормированным базисом ![]() . Единичные векторы ē1 ={m1, n1}, ē2{m2, n2} примем за направляющие векторы новых осей координат системы
. Единичные векторы ē1 ={m1, n1}, ē2{m2, n2} примем за направляющие векторы новых осей координат системы ![]() , ē1 ┴ ē2.
, ē1 ┴ ē2.
Пусть новая система координат, определяемая базисом ē1, ē2 повернута на угол α относительно старой системы координат, определяемой базисом ![]() .
.
Матрица В =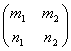 , составленная из координат векторов ē1 и ē2, является матрицей перехода к новому базису.
, составленная из координат векторов ē1 и ē2, является матрицей перехода к новому базису.
Координаты нового базиса ē1, ē2 относительно старого базиса ![]() будут:
будут:
![]() и, следовательно, матрица перехода к новому базису имеет вид:
и, следовательно, матрица перехода к новому базису имеет вид:
B=![]() и B-1=
и B-1=![]()
В данном случае транспонированная матрица совпадает с обратной.
X=BX‘, ![]() =
=![]()
![]()
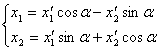 (5) и
(5) и 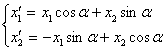 (5’)
(5’)
Полученные формулы (5) и (5/) являются формулами преобразования координат при повороте осей координат.
Ортогональная матрица.
Пусть элементы матрицы В = 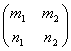 удовлетворяют условиям m12+n12=1; m22+n22=1; m1n1+m2n2=0, тогда
удовлетворяют условиям m12+n12=1; m22+n22=1; m1n1+m2n2=0, тогда
BBt=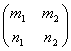
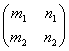 =
=![]() =E и BtB=E,
=E и BtB=E,
то есть транспонированная матрица совпадает с обратной. Тогда матрица В называется ортогональной.
Квадратичные формы. Приведение к каноническому виду.
Квадратичной формой переменных х1, х2 называется выражение
s(x1, x2)=a11x12+2a12x1x2+a22x22 (6).
Канонический вид квадратичной формы
s*(x1, x2)=l1 x12+l2x22 . (7)
Рассмотрим матрицы квадратичных форм (6) и (7)
А =  , В=
, В=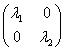 и вектор
и вектор 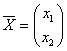 .
.
Матричная запись квадратичной формы (6)
s(x1, x2)=![]() A
A ![]() ,
,
и соответственно для формы (7)
s*(x1, x2)= ![]() В
В![]() .
.
Теорема. Квадратичная форма с матрицей А является канонической в базисе ē1, ē2 , где ē1, ē2 - единичные, взаимно перпендикулярные собственные векторы матрицы А.
Действительно, s(x1, x2)=![]() A
A ![]() , в базисе
, в базисе ![]() .
.
Перейдем от базиса ![]() к базису (ē1, ē2), тогда формулы перехода
к базису (ē1, ē2), тогда формулы перехода
![]() =B
=B![]() ’, где В=
’, где В=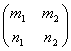 - матрица из координат собственных векторов.
- матрица из координат собственных векторов.
В новом базисе ē1, ē2 матрица B-1AB= 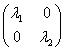 , где λ1 ,λ2 соответствующие собственные значения, отсюда следует s*(x1, x2)=
, где λ1 ,λ2 соответствующие собственные значения, отсюда следует s*(x1, x2)= ![]() =l1x’12+lx’22.
=l1x’12+lx’22.
Приведение общего уравнения линии 2-го порядка к
каноническому виду.
Общее уравнение линии 2-го порядка
a11x12+2a12x1x2+a22x22 +2a13x1+2a23x2+a33=0.
По группе старших членов составляем определитель
d=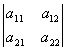 , a12=a21, d=a11a22-a122.
, a12=a21, d=a11a22-a122.
1) δ > 0 – кривая эллиптического типа
2) δ < 0 – кривая гиперболического типа
3) δ = 0 – кривая параболического типа
Схема приведения кривой к каноническому виду:
1) По группе старших членов составляем матрицу А=  .
.
2) Характеристическое уравнение |A – λ E| = 0.
Определяем собственные значения и собственные векторы матрицы А.
А ē = λ ē (ē1(m1,n1) и ē2(m2,n2), I ē1I= I ē2I=1).
3) Cоставляем матрицу перехода к новому базису В = 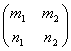 .
.
4) Выписываем преобразование координат при повороте осей координат ![]() =B
=B![]() ’.
’.
5) В новом базисе ē1, ē2 группе старших членов соответствует λ1X’1 2+ λ2X’ 22.
6) Выделяем полные квадраты членов с каждой из координат, так определяем центр, в случае центральных кривых и вершину в случае параболы.
7) Строим график кривой.
Задачи на темы ”Собственные векторы ”, “Приведение кривой к каноническому виду”.
Пример 1. Найти собственные числа и собственные вектора матрицы
А=![]() .
.
Решение. 1. Решим характеристическое уравнение IА-lЕI=0. В нашем случае оно имеет вид:
![]() =0, то есть l2-13l+22=0.
=0, то есть l2-13l+22=0.
Собственными числами являются корни характеристического уравнения l1=2, l2=11.
2. Собственный вектор ![]() 1, соответствующий числу l1=2, является базисом в пространстве решений однородной системы
1, соответствующий числу l1=2, является базисом в пространстве решений однородной системы
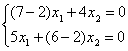 .
.
Эта система состоит из двух одинаковых уравнений, где неизвестные x1, x2 связаны зависимостью
5x1+4x2=0, или x1=![]() x2.
x2.
Положив параметрическую неизвестную x2 равную произвольной константе, например 1, получим x1=![]() и собственный вектор
и собственный вектор ![]() 1=
1=![]() .
.
3. Для собственного вектора ![]() 2, соответствующую l2=11, составим систему
2, соответствующую l2=11, составим систему
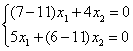 .
.
Решая ее, придем к соотношению x1-x2=0, или x1=x2.
Положив x2=1, получим ![]() 2=
2=![]() .
.
Пример 2. Привести уравнение кривой 5х12 + 8х1х2 + 5х22 – 18х1 – 18х2 + 9 = 0 к каноническому виду. Решение. Составляем определитель δ =![]() =25-16=9>0. Следовательно, кривая эллиптического типа.
=25-16=9>0. Следовательно, кривая эллиптического типа.
1) Матрица группы старших членов А = ![]() .
.
2) Характеристическое уравнение: IА-lЕI=0, ![]() =0.
=0.
Отсюда ( 5-λ)2 – 16 = 0 λ1=9; λ2=1.
![]()
при l1=9 ![]() , следовательно, при m=n
, следовательно, при m=n ![]() {1;1}, I
{1;1}, I![]() I=
I=![]() ,
, ![]() ,
,
при l2=1 ![]() , следовательно, при m= - n
, следовательно, при m= - n ![]() {-1;1}, I
{-1;1}, I![]() I=
I=![]() ,
, ![]() ,
,
3) Матрица перехода к новому базису В = 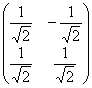 .
.
4) Преобразование координат при переходе к новому базису
![]() =B
=B![]() ’ или
’ или ![]() =
=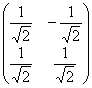
![]() ,
,
формулы преобразования поворота осей координат (перехода к новому базису):
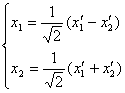 .
.
5) В новом базисе уравнение линии
![]() ,
,
![]() ,
,
![]() ,
,
![]()
6) В новой системе координат центр в точке О1(![]() ; 0), полуоси а=1, b=3.
; 0), полуоси а=1, b=3.
7) Cтроим график кривой.
