Лекция 6. Системы линейных алгебраических уравнений.
Однородные системы линейных уравнений.
Матрица А, составленная из коэффициентов при неизвестных
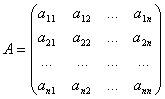 называется матрицей системы.
называется матрицей системы.
Числа, стоящие в правых частях уравнений, образуют столбец ![]() , называемый столбцом свободных членов.
, называемый столбцом свободных членов.
Матрица системы, дополненная справа столбцом свободных членов, называется расширенной матрицей системы
В=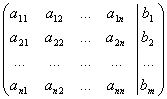 .
.
Если свободные члены всех уравнений равны нулю, то система называется однородной.
Определение. Совокупность n чисел х10,х20,…хn0 называется решением системы (1), если каждое уравнение системы обращается в числовое равенство после подстановки в него чисел (х10,х20,…хn0) вместо соответствующих неизвестных (х1,х2,…хn ).
Системы, не имеющие решений, называются несовместными, а имеющие решения – совместными.
Методы решения системы линейных алгебраических уравнений.
1. Правило Крамера.
Система из n неизвестных уравнений с n неизвестными
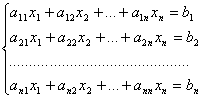 (1)
(1)
в случае , когда детерминант (определитель) матрицы системы отличается от нуля, имеет решение, и притом только одно. Это решение находится по формулам:
xi=![]() (для всех I=1,2,…,n), где через D обозначен определитель матрицы системы, а через Dxi- определитель, получаемый из определителя системы заменой I- того столбца столбцом свободных членов, то есть
(для всех I=1,2,…,n), где через D обозначен определитель матрицы системы, а через Dxi- определитель, получаемый из определителя системы заменой I- того столбца столбцом свободных членов, то есть
Dxi=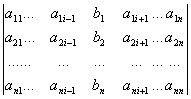 , i=1,2,…,n.
, i=1,2,…,n.
2. Решение системы методом обратной матрицы.
Рассматривается система вида (1) из n линейных уравнений с n неизвестными. Пусть определитель системы не равен нулю. Представим систему (1 ) в матричном виде
AX=B (2), где
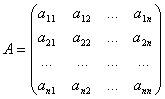 матрица системы ,
матрица системы , 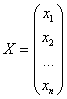 матрица-столбец неизвестных,
матрица-столбец неизвестных, 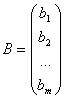 ,матрица-столбец свободных членов
,матрица-столбец свободных членов
Так как det(A)¹0, то для матрицы А существует обратная матрица А-1. Умножим обе части уравнения (2 ) слева на А-1, получим решение системы (1) в матричном виде:
X=A-1B. (3)
3. Метод Гаусса.
С помощью элементарных преобразований строк приведем матрицу размера n´n к треугольному виду:
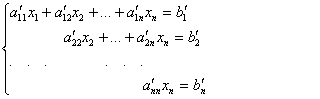
Затем начинается, так называемый “обратный ход”: из последнего уравнения системы определяется xn , подставляем это значение в предпоследнее уравнение, определяем xn-1 и так далее, пока из первого уравнения не определим x1.
Пример. Дана система:
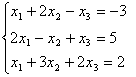
Найти решение: 1. по формулам Крамера,
2. методом обратной матрицы ,
3. методом Гаусса.
Решение:1. по формулам Крамера:
D=det(A)=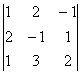 =1
=1![]() -2
-2![]() -1
-1![]() =-18 ¹0.
=-18 ¹0.
Dx1=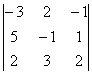 = -3
= -3![]() -2
-2![]() -1
-1![]() =-18 , x1=
=-18 , x1=![]() =1.
=1.
Dx2=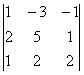 =1
=1![]() +3
+3![]() -1
-1![]() =18 , x2=
=18 , x2=![]() = -1.
= -1.
Dx3=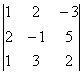 =1
=1![]() -2
-2![]() -3
-3![]() = -36 , x2=
= -36 , x2=![]() = 2.
= 2.
Ответ:{1; -1;2}.
2.методом обратной матрицы.
D=det(A)=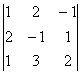 = -18 .
= -18 .
Так как det(A)¹0, то по теореме об обратной матрице, ![]() определена.
определена.
Найдем алгебраические дополнения соответствующих элементов определителя det(A):
| A11= |
A21= - |
A31= |
| A12=- |
A22= |
A32=- |
| A13= |
A23=- |
A33= |
Строим союзную матрицу ![]() :
:
![]() =
=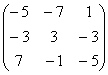 .
.
Следовательно, ![]() =
=![]()
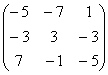
Итак, решением системы будет
X=A-1B= ![]()
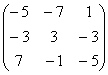
![]() =
=![]()
![]() =
=![]() , отсюда x1=1, x2=-1, x3=2.
, отсюда x1=1, x2=-1, x3=2.
1.методом Гаусса.
Выпишем расширенную матрицу системы:
C=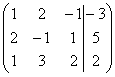 ~C2-2C1, C3-C1
~C2-2C1, C3-C1 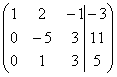 ~C2+5C3
~C2+5C3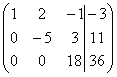 ~C3:18
~C3:18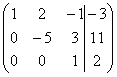
Получаем систему треугольного вида:
x1 + 2x2 – x3 = -3
-5x2 + 3x3 = 11
x3 = 2
Отсюда x3=2
-5x2+6=11 Þ x2= -1,
x1+2x2-x3= -3 Þx1-2-2=-3, x1=1.
Ответ:{1; -1;2} ![]()
Замечание: C помощью элементарных преобразований, матрицу А можно привести к диагональному виду, а затем к единичной матрице.
Продолжим преобразование матрицы С:
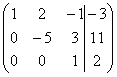 ~C1+C3, C2-3C3
~C1+C3, C2-3C3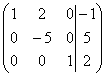 ~C2:(-5)
~C2:(-5) ~C1-2C2
~C1-2C2 .
.
Отсюда x1=1, x2=-1, x3=2.
Множество решений однородной системы.
Рассмотрим однородную систему m уравнений с n неизвестными:
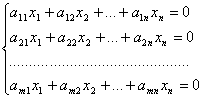 (1).
(1).
Однородная система линейных уравнений всегда совместна, т.к. одним из решений является тривиальное уравнение (0,0,….0)
Предложение. Если однородная система (1) имеет два решения X= (х1,х2,…хn) и Y=(y1, y2,…. yn ), то любая линейная комбинация решений Z также решение: Z=a![]() .
.
Рассмотрим матрицу системы (1)
A=
Применяя элементарные преобразования строк приведем матрицу А к упрощенному виду:
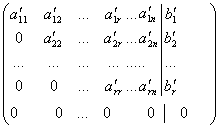 Отсюда r(A)= r и D=
Отсюда r(A)= r и D=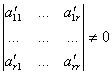 базисный минор.
базисный минор.
Данная нам система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений:
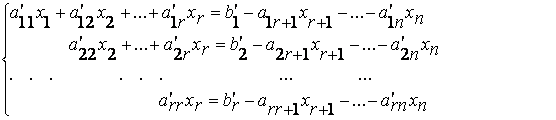 (2)
(2)
В левых частях равенств мы оставили неизвестные, соответствующие столбцам базисного минора , так называемые базисные неизвестные. Остальные неизвестные – называемые параметрическими – перенесены в правые части равенств.
Всего параметрических неизвестных n – r.
Тогда решая систему (2), например, по формулам Крамера, получили:
 (3).
(3).
Параметрическим неизвестным задаем значения по схеме:
1)xr+1=1, xr+2=0, …, xn=0,
2)xr+1=0, xr+2=1, …, xn=0, (4)
… … …
n-r) xr+1=0, xr+2=0, … xn=1.
Для каждой совокупности значений параметрических неизвестных найдем из системы (3) соответствующие базисные неизвестные:
1)x11, x12, …, x1r,
2)x12, x22, …, x2r,
… … …
n-r) xn-r 1, xn-r 2, …, xn-r r.
Получаем n – r решений системы (1):
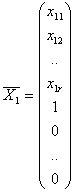 ,
, 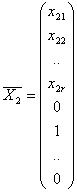 , …,
, …, 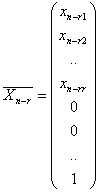 (5).
(5).
Эти решения линейно независимы, т.к. матрица из их столбцов имеет минор порядка n-r, равный единице.
Совокупность решений (5) называется нормальной фундаментальной системой решений.
Тогда любое решение линейной однородной системы представляет собой линейную комбинацию нормальной фундаментальной системы решений:
![]() , где с1, c2, …,cn-r –произвольные постоянные.
, где с1, c2, …,cn-r –произвольные постоянные.
Общая теория линейных систем.
Рассмотрим линейную неоднородную систему m уравнений с n неизвестными:
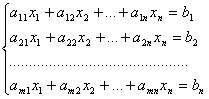 (6)
(6)
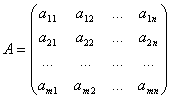 Матрица системы
Матрица системы
 Расширенная матрица
Расширенная матрица
Теорема о базисном миноре позволяет дать условие совместности системы линейных уравнений (6), носящее название
Теорема Кронекера-Капелли.
Система (1) имеет хотя бы одно решение в том и только в том случае, когда ранг матрицы системы А равен рангу расширенной матрицы А*, т.е. r(А) = r(А*).
Общая схема исследования и решения системы (6).
1)Составляем расширенную матрицу системы А*.
2)С помощью элементарных преобразований приводим матрицу А* к упрощенному треугольному виду.
3)Сравниваем ранги матрицы А и А*.
Если: 1)r(А) ≠ r(А*), то система несовместна,
2)r(А) = r(А*), то система совместна.
Пусть система (1) совместна и r(А) = r(А*) = r.
Мы можем выбрать базисный минор расширенной матрицы так, чтобы он был расположен в матрице системы. Данная нам система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.
Для удобства записи будем предполагать, что базисный минор расположен в первых r столбцах, тогда преобразованную систему можно записать в виде:
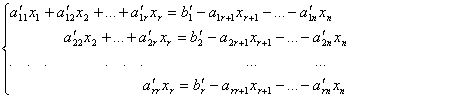 (7).
(7).
x1, x2,…,xr-базисные неизвестные, xr+1, xr+2,…, xn-параметрические неизвестные, их всего n-r.
Параметрические неизвестные обычно задаются по схеме (4), а базисные неизвестные определяются из системы (7). Этим способом мы получим всю совокупность решений.
Общее решение системы линейных уравнений.
Теперь мы можем собрать воедино наши результаты.
Теорема. Если 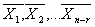 – фундаментальная система решений системы (7), а
– фундаментальная система решений системы (7), а 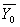 - некоторое частное решение системы (6), то общее решение системы линейных алгебраических неоднородных уравнений (6):
- некоторое частное решение системы (6), то общее решение системы линейных алгебраических неоднородных уравнений (6):
![]() (8), при любых с1, с2,…сn-r.
(8), при любых с1, с2,…сn-r.
Наоборот, для каждого решения этой системы найдутся такие числа с1, …сn-r, при которых решение имеет вид (8) или в развернутом виде:
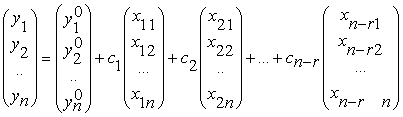 (9).
(9).
Выражение, стоящее в правой части равенства (9), называется общим решением системы линейных неоднородных уравнений (6).
Задачи на тему “Системы линейных алгебраических уравнений”.
Определить размерность пространства решений, найти базис (фундаментальную систему решений) и общее решение следующих систем:
1)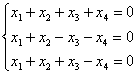 , 2)
, 2) 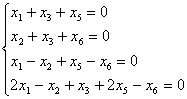 ,
,
3) 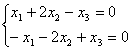 , 4)
, 4) 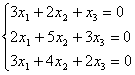 .
.
Для каждого из рассматриваемых случаев составим матрицу системы, с помощью элементарных операций преобразуем ее к приведенной форме, то есть, последовательно сформируем на главной (или смещенной) диагонали единицы, а выше и ниже диагонали нули. После чего, определим ранг и найдем решение системы.
![]() 1) А=
1) А=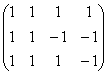 ~C2-C1, C3-C1
~C2-C1, C3-C1 ~C2;(-2), C3(-2) ~
~C2;(-2), C3(-2) ~ .
.
Вторым элементом главной диагонали является ноль, а нам нужен не нулевой элемент, чтобы получить на диагонали единицу, поэтому здесь необходимо рассмотреть смещенную диагональ. Элементарными преобразованиями С1-С2 и С2-С3 преобразуем эту матрицу к приведенной форме:
Отсюда, ранг исследуемой матрицы А: r(A)=3.
Пространство решений ![]() имеет размерность L=n-r=4-3=1,где n=4-число неизвестных системы, и содержит один базисный вектор
имеет размерность L=n-r=4-3=1,где n=4-число неизвестных системы, и содержит один базисный вектор ![]() . Чтобы найти базисный вектор, восстановим по приведенной матрице систему:
. Чтобы найти базисный вектор, восстановим по приведенной матрице систему:
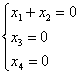 ,
,
и выразим базисные неизвестные x1, x3, x4, соответствующие элементам смещенной диагонали, через параметрическое неизвестное x2;
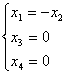 .
.
В полученной системе положим x2=1, будем иметь:
![]() =
=![]() Базисный вектор,
Базисный вектор, 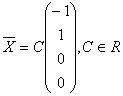 Пространство решений однородной системы.
Пространство решений однородной системы.
2) A= ~ C3-C1, C4-2C1
~ C3-C1, C4-2C1 ~
~
~C3+C2, C4+C2 ~
~![]() .
.
Таким образом, ранг матрицы А: r(A)=2, размерность пространства решений L=6-2=4.
Восстановим по последней матрице систему:
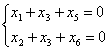
и выразим базисные неизвестные x1, x2 через параметрические x3, x4, x5, x6:
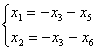 .
.
Найдем теперь фундаментальную систему решений, состоящую из четырех(L=4) векторов, полагая,
для ![]() 1: x3=1, x4=0, x5=0, x6=0;
1: x3=1, x4=0, x5=0, x6=0;
для ![]() 2: x3=0, x4=1, x5=0, x6=0;
2: x3=0, x4=1, x5=0, x6=0;
для ![]() 3: x3=0, x4=0, x5=1, x6=0;
3: x3=0, x4=0, x5=1, x6=0;
для ![]() 4: x3=0, x4=0, x5=0, x6=1,
4: x3=0, x4=0, x5=0, x6=1,
имеем:
![]() 1=
1=![]() ,
, ![]() 2=
2=![]()
![]() 3=
3=![]()
![]() 4=
4=![]()
Фундаментальная система решений.
и ![]() =C1
=C1![]() +C2
+C2![]() +C3
+C3![]() +C4
+C4![]() ; C1 ,C2, C3, C4
; C1 ,C2, C3, C4 ![]() R.
R.
Пространство решений однородной системы, являющееся линейной комбинацией базисных векторов
3) A=![]() ~C2+C1
~C2+C1![]() ~
~![]() ,
,
r(A)=1, L=3-1=2.
Восстановим систему и выразим единственную базисную неизвестную x1 через параметрические x2, x3;
X1=-2x2+x3.
Теперь полагая
для ![]() 1: x2=1, x3=0
1: x2=1, x3=0
для ![]() 2: x2=0, x3=1, получим:
2: x2=0, x3=1, получим:
![]() 1=
1=![]() ,
, ![]() 2=
2=![]() и
и 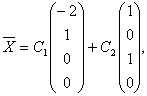 C1,C2
C1,C2![]() R.
R.
4) A=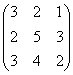 ~ C1-C2, C3-C2
~ C1-C2, C3-C2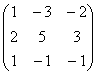 ~ C2-2C1, C3-C1 ~
~ C2-2C1, C3-C1 ~ ~C2-5C3 ~
~C2-5C3 ~ ~ C1+3C2, C3-2C2
~ C1+3C2, C3-2C2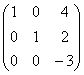 ~C3:(-3) ~
~C3:(-3) ~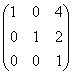 ~ C1-4C3, C2-2C3 ~
~ C1-4C3, C2-2C3 ~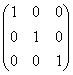 .
.
| Ранг матрицы А однородной системы r(A)=3. Пространство решений имеет размерность L=3-3=0 и поэтому не содержит базисных векторов и состоит только из нулевого вектора: |
|
Неоднородные системы линейных алгебраических уравнений (СЛАУ).
Исследовать систему и в случае совместности найти ее решения.
1) 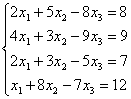 , 2)
, 2) 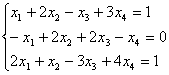 ,
,
3) 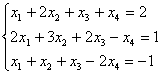 4)
4) 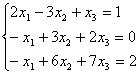 .
.
Исследование системы будем проводить в следующем порядке:
1)Составим расширенную матрицу системы (АIb) и с помощью элементарных преобразований получим ее приведенную форму.
2)Найдем ранги r(A), r(AIb) и по теореме Кронекера-Капелли сделаем выводы.
Если система неопределена, то переходим к пункту 3 и продолжим изучение.
3)По приведенной матрице А восстановим однородную систему уравнений и найдем ее множество решений X00.
4)По приведенной расширенной матрице (АIb) восстановим неоднородную систему уравнений и, положив параметрические неизвестные равными, например, нулю, найдем частное решение Xч.н..
5)Общее решение неоднородной системы представляет собой сумму общего однородного и частного неоднородного решений, то есть Xо.н.=Xо.о+Xч.н..
![]() 1)
1)
1(AIb)=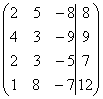 ~C1-C4
~C1-C4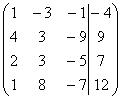 ~ C2-4C1, C3-2C1, C4-C1,
~ C2-4C1, C3-2C1, C4-C1,
~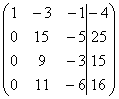 ~C2:5, C3:3
~C2:5, C3:3 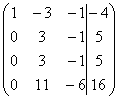 ~ C3-C2, C4-4C2 ~
~ C3-C2, C4-4C2 ~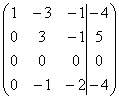 ~ C2+2C4
~ C2+2C4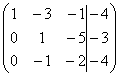 ~ C1+3C2, C3+C2 ~
~ C1+3C2, C3+C2 ~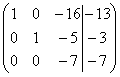 ~C3(-7)
~C3(-7) 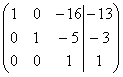 ~ C1+16C3, C2+5C3 ~
~ C1+16C3, C2+5C3 ~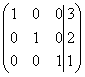 .
.
2.Определитель 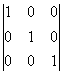 =1
=1![]() 0 является для матриц А и (AIb) базисным минором, поэтому r(A)=r(AIb)=3 и по теореме Кронекера-Капелли исходная система уравнений совместна. Так как число неизвестных n=3 совпадает с рангом r(AIb), то система имеет единственное решение, то есть определена. Это решение найдем восстановив систему по приведенной матрице (AIb):
0 является для матриц А и (AIb) базисным минором, поэтому r(A)=r(AIb)=3 и по теореме Кронекера-Капелли исходная система уравнений совместна. Так как число неизвестных n=3 совпадает с рангом r(AIb), то система имеет единственное решение, то есть определена. Это решение найдем восстановив систему по приведенной матрице (AIb):
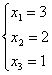 .
.
2)1.
(AIb)=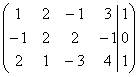 ~C2+C1 , C3-2C1
~C2+C1 , C3-2C1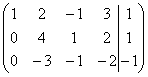 ~ C2+C3 , C3(-1)
~ C2+C3 , C3(-1)
~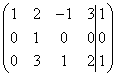 ~C1-2C2 , C3-3C2
~C1-2C2 , C3-3C2 ~C1+C3
~C1+C3 .
.
2.Матрица А имеет базисный минор  , следовательно, r(A)=3. Ранг расширенной матрицы также равен 3, так как рассмотренный выше минор является базисным минором и для матрицы (АIb).
, следовательно, r(A)=3. Ранг расширенной матрицы также равен 3, так как рассмотренный выше минор является базисным минором и для матрицы (АIb).
Итак, по теореме Кронекера-Капелли исходная система совместна. Поскольку число неизвестных системы п=4 больше, чем r(AIb), то система имеет бесконечно много решений, то есть является неопределенной.
3.Однородная система имеет вид:
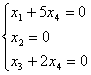 .
.
Так как r(A)=3, n=4, то размерность пространства решений однородной системы L=r(A)-n=4-3=1 и существует только один базисный вектор ![]() 1. Координаты этого вектора получаются из равенств:
1. Координаты этого вектора получаются из равенств:
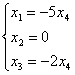 ,
,
если положить в них параметрическую переменную x4 равную 1. Имеем,
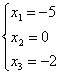 и
и ![]() 1=
1=![]() , X00=C
, X00=C![]() , C
, C![]() R.
R.
4.Неоднородная система имеет вид:
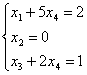 . Полагая здесь X4=0, получим:
. Полагая здесь X4=0, получим: 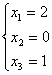 и Xч.н.=
и Xч.н.= ![]() .
.
5.Общее решение исходной системы имеет вид:
Xо. н.=C![]() +
+![]() , C
, C![]() R.
R.
3) 1. (AIb)=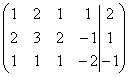 ~C2-2C1 , C3-C1
~C2-2C1 , C3-C1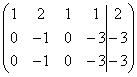 ~ C2 (-1), C3+C2 ~
~ C2 (-1), C3+C2 ~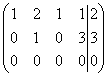 ~ C1-2C1
~ C1-2C1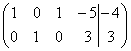 .
.
2. Определитель ![]() =1
=1![]() 0 является для матриц А и (АIb) базисным минором, поэтому r(A)=r(AIb)=2. По теореме Кронекера-Капелли система уравнений совместна, и так как число неизвестных п=4 больше ранга r(AIb), то система неопределена.
0 является для матриц А и (АIb) базисным минором, поэтому r(A)=r(AIb)=2. По теореме Кронекера-Капелли система уравнений совместна, и так как число неизвестных п=4 больше ранга r(AIb), то система неопределена.
3.Однородная система имеет вид
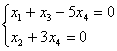 или
или 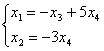 .
.
Так как r(A)=2, п=4, то пространство решений однородной системы имеет размерность L=4-2=2 и содержит два базисных вектора ![]() 1,
1, ![]() 2. Полагая в последней системе уравнений параметрические неизвестные x3=1, x4=0, получим
2. Полагая в последней системе уравнений параметрические неизвестные x3=1, x4=0, получим
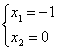 ,
, ![]() 1=
1=![]() , и x3=0, x4=1, получим
, и x3=0, x4=1, получим 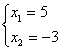 ,
, ![]() 2=
2=![]() .
.
Общее решение однородной системы: X00=С1![]() +С2
+С2![]() , C1,C2
, C1,C2![]() R.
R.
4.Неоднородная система имеет вид
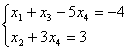 . Полагая здесь x3=x4=0, получим
. Полагая здесь x3=x4=0, получим 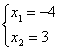 и частное решение Xx.н.=
и частное решение Xx.н.= ![]() .
.
5.Общее решение исходной системы:
Xo.н.=C1![]() +С2
+С2![]() +
+![]() , C1,C2
, C1,C2![]() R.
R.
4) 1 (AIb)=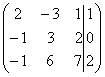 ~ C1+C2 , C3-C2
~ C1+C2 , C3-C2 ~ C2+C1 ~
~ C2+C1 ~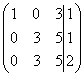 ~
~
~ C3-C2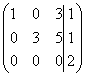 .
.
2. Матрица А~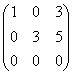 ~
~![]() имеет базисный минор
имеет базисный минор ![]() второго порядка, следовательно, r(A)=2. Ранг расширенной матрицы (AIb)=
второго порядка, следовательно, r(A)=2. Ранг расширенной матрицы (AIb)= 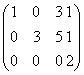 равен трем, поскольку ее минор
равен трем, поскольку ее минор 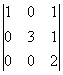 =6
=6![]() 0.
0.
Итак, r(A)![]() r(AIb), стало быть, по теореме Кронекера-Капелли исследуемая система уравнений не имеет решений, то есть несовместна.
r(AIb), стало быть, по теореме Кронекера-Капелли исследуемая система уравнений не имеет решений, то есть несовместна.
 .
.