Лекция 5. Линейная алгебра.
Матрицы.
Определение. Матрицей размера m x n называется совокупность ![]() элементов (чисел), расположенных в виде таблицы из m строк и n столбцов:
элементов (чисел), расположенных в виде таблицы из m строк и n столбцов:

или короче: ![]() , 1
, 1![]() m, 1
m, 1![]() n, где i – номер строки, j-номер столбца.
n, где i – номер строки, j-номер столбца.
Если число строк в матрице равно числу столбцов, то матрица называется квадратной, а число строк ее порядком. Остальные матрицы носят название прямоугольных.
Обозначаются матрицы заглавными буквами русского и латинского алфавитов.
Частные виды матриц:
- Матрица с любым числом строк и столбцов, все элементы которой равны нулю, называется нуль-матрицей ,
- Матрица - строка В=(b1, b2, … bn),
- Матрица - столбец
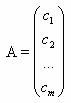
4.Детерминант квадратной матрицы – это ее определитель:  .
.
- Элементы
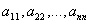 образуют главную диагональ матрицы.
образуют главную диагональ матрицы. - Диагональная матрица – это квадратная матрица, у которой все элементы равны нулю, за исключением, быть может, элементов главной диагонали.
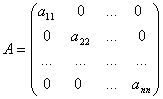 или
или 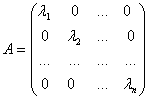 .
.
- Если все λi = 1, i = 1,2…n , то диагональная матрица называется единичной и обозначается:
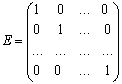 .
.
Определение.
- Матрицы А и В называются матрицами одинаковых размеров, если соответственно равны числа строк и столбцов, т.е. их порядки равны.
- Две матрицы называются равными. Если они имеют одинаковые размеры и равны. их элементы, стоящие на одинаковых местах.
Линейные операции над матрицами.
1. Сложение матриц.
Суммой двух прямоугольных матриц А и В, имеющих одинаковые размеры, называется матрица С, элементами которой являются суммы соответствующих элементов матриц А и В .
С = А + В , где А =![]() , B=
, B=![]() , C=
, C=![]() , cik=aik+bik , 1£ i£ m, 1£ k£ n .
, cik=aik+bik , 1£ i£ m, 1£ k£ n .
Сложение матриц подчиняется следующим законам:
1.А+В = В+А (коммутативность),
2.А+(В+С) = (А+В)+С (ассоциативность),
3.Если 0-ноль матрица, то А+О = А.
Разность двух матриц определяется как алгебраическая сумма матриц.
Матрицу (-1)А называют противоположной матрице А и обозначают –А. Она обладает тем свойством, что А+(-А)=0.
2. Умножение матрицы на число.
Матрица С =![]() , элементы которой 1£ i£ m, 1£ k£ n, (сik) равны произведению элементов аik матрицы А на число
, элементы которой 1£ i£ m, 1£ k£ n, (сik) равны произведению элементов аik матрицы А на число ![]() , называется произведением А на
, называется произведением А на ![]() и обозначается αА.
и обозначается αА.
Мы имеем cik = ![]() аik .
аik .
Умножение матрицы на число подчиняется следующим законам:
α(А+В) = αА+αВ; (α+β)А=αА+βА; (αβ)А=α(βА).
3. Транспонирование матриц.
Если в данной матрице А, поменять местами столбцы и строки, то получают транспонированную матрицу Аt.
Симметричная матрица – это квадратная матрица, совпадающая со своей транспонированной матрицей.
А =![]() , At=
, At= ![]() , aik=aki, 1£ i£ n, 1£ k£ n, то есть At=A.
, aik=aki, 1£ i£ n, 1£ k£ n, то есть At=A.
4. Умножение матриц.
Произведение матриц А и В обозначается С=А×В. В общем случае А×В ≠ В×А.
Пусть матрица А=![]() , 1£ i£ m, 1£ k£ n размера m´n, B=
, 1£ i£ m, 1£ k£ n размера m´n, B=![]() 1£ k£ n, 1£ j£ p размера n´p.
1£ k£ n, 1£ j£ p размера n´p.
Произведением А´В назовем матрицу С=![]() , 1£ i£ m, 1£ j£ p (размера m´p), элементы которой определяются по правилу:
, 1£ i£ m, 1£ j£ p (размера m´p), элементы которой определяются по правилу:
![]()
Свойства произведения матриц.
Если для некоторых матриц АВ=АВ, то матрицы А и В называются коммутативными или перестановочными. Например, ЕА=АЕ=А, где Е единичная матрица, А- квадратная матрица.
Операция умножения матриц подчиняется сочетательному и распределительному законам умножения:
1. (А×В)×С=А×(В×С);
2. А×(В+С)=А×В+А×С;
3. (А+В)×С=А×С+В×С.
5. Обратная матрица.
Пусть матрица А – квадратная, порядка n. Левой обратной матрицей по отношению к матрице А называется матрица ![]() того же порядка n, удовлетворяющего равенству
того же порядка n, удовлетворяющего равенству
![]() А = Е.
А = Е.
Аналогично определяется правая обратная матрица ![]() , удовлетворяющая равенству: А
, удовлетворяющая равенству: А![]() =Е.
=Е.
Если левая и правая обратные матрицы совпадают , то это есть обратная матрица:
![]() =
=![]() =А-1
=А-1
Условием существования обратной матрицы для данной квадратной матрицы является условие d(А)≠0, т.е. матрица не особая. Если матрица А имеет обратную, то эта матрица единственная.
Как найти обратную матрицу:
1.Пусть дана матрица 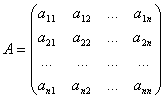 и d(А)≠0.
и d(А)≠0.
2.Союзная матрица ![]() - это транспонированная матрица алгебраических дополнений элементов данной матрицы. Элементу аiк соответствует алгебраическое дополнение Аiк, тогда
- это транспонированная матрица алгебраических дополнений элементов данной матрицы. Элементу аiк соответствует алгебраическое дополнение Аiк, тогда
 и обратная матрица
и обратная матрица ![]() .
.
Известно, что сумма произведений элементов некоторого ряда на их алгебраические дополнения равна определителю, а сумма произведений элементов некоторого ряда на алгебраические дополнения соответствующих элементов другого ряда равна нулю, поэтому
А-1 А=![]()
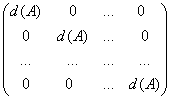 =
= =E.
=E.
Свойства столбцов матрицы А.
Пусть матрица А = ![]() , 1£ i£ m, 1£ k£ n.
, 1£ i£ m, 1£ k£ n.
Определение. Система из s столбцов ![]() ,…,
,…, ![]() матрицы А называется линейно зависимой если существует набор чисел
матрицы А называется линейно зависимой если существует набор чисел ![]() одновременно не равных нулю, для которых линейная комбинация равна нулю
одновременно не равных нулю, для которых линейная комбинация равна нулю
![]() .
.
В противном случае система столбцов ![]() ,…,
,…, ![]() линейно независимая, т.е. линейная комбинация равна нулю только при всех коэффициентах
линейно независимая, т.е. линейная комбинация равна нулю только при всех коэффициентах![]() одновременно равных нулю.
одновременно равных нулю.
Предложение 1. Система 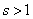 столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
Предложение 2 . Если в систему столбцов входит нулевой столбец, то система линейно зависима.
Предложение 3. Если в системе из k столбцов к-1 столбцов линейно зависимы, то и k столбцов линейно зависимы.
Предложение 4 . Любые столбцы, входящие в линейно независимую систему, сами по себе образуют линейно независимую систему.
Предложение 5 . Если столбец ![]() есть линейная комбинация столбцов
есть линейная комбинация столбцов ![]() ,…,
,…, ![]() , то он является также линейной комбинацией любой системы столбцов, содержащей
, то он является также линейной комбинацией любой системы столбцов, содержащей ![]() ,…,
,…, ![]() .
.
Предложение 6. Если А квадратная матрица и detА= 0, то один из столбцов есть линейная комбинация остальных столбцов.
Базисный минор.
Определение. В матрице А размером m´ n минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка ![]() равны нулю, или миноров порядка
равны нулю, или миноров порядка ![]() вообще нет, т.е. r совпадает с n или m.
вообще нет, т.е. r совпадает с n или m.
Определение. Ранг – это порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Обозначение ранга r( А).
Дадим еще одно определение ранга:
Определение. Матрица А имеет ранг ко, если среди миноров порядка ко есть хотя бы один отличный от нуля, а все миноры более высокого порядка (ко+1 и т.д.) равны нулю.
Основные теоремы.
Теорема 1. В произвольной матрице А каждый столбец, не входящий в ее базисный минор, является линейной комбинацией столбцов, в которых расположен базисный минор.
Теорема 2. (о ранге матрицы). Ранг матрицы А равен максимальному числу линейно независимых столбцов этой матрицы.
Элементарные преобразования матриц.
К элементарным преобразованиям матриц относятся следующие преобразования:
1. Умножение строки на число, отличное от нуля.
2. Прибавление к одной строке другой строки.
3. Перестановка строк.
4. Те же преобразования столбцов.
Элементарные преобразования не меняют ранга матрицы (базисный минор сохраняется в виде, отличном от нуля).
Задачи на тему “Матрицы”.
1)Найти матрицу С=3Аt-2В, где
А=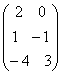 , B=
, B=![]() .
.
![]() 1. Найдем транспонированную матрицу Аt. Для этого в матрице А поменяем местами строки и столбцы:
1. Найдем транспонированную матрицу Аt. Для этого в матрице А поменяем местами строки и столбцы:
Аt=![]() .
.
2. Все элементы матрицы Аt умножим на 3, а элементы матрицы В на 2, получим:
3At=![]() , 2B=
, 2B=![]() .
.
3. Матрица С есть результат вычитания от элементов матрицы 3Аt соответствующих элементов матрицы 2В:
C=![]() .
. ![]()
2)Найти произведение матриц АВ:
1.A=![]() , B=
, B=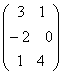 ;
;
2.A=![]() , B=
, B=![]() ;
;
3.A=![]() , B=
, B=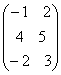 ;
;
4.A=![]() , B=
, B=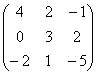 .
.
![]() Заметим, что во всех случаях рассматриваемой задачи, для матриц АВ выполнено условие согласования, то есть, количество столбцов матрицы А совпадает с количеством строк матрицы В, следовательно, АВ определена.
Заметим, что во всех случаях рассматриваемой задачи, для матриц АВ выполнено условие согласования, то есть, количество столбцов матрицы А совпадает с количеством строк матрицы В, следовательно, АВ определена.
1.Так как А(2![]() 3), В(3
3), В(3![]() 2), то АВ(2
2), то АВ(2![]() 2) и
2) и
АВ=![]()
 =
=![]() = =
= =![]() .
.
2.Так как А(2![]() 3), В(3
3), В(3![]() 1), то АВ(2
1), то АВ(2![]() 1) и
1) и
АВ=![]()
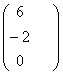 =
=![]() =
=![]() .
.
3.Так как А(1![]() 3), В(3
3), В(3![]() 2), то АВ(1
2), то АВ(1![]() 2) и
2) и
АВ=![]()
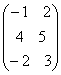 =
=![]() =(15 11).
=(15 11).
4.Так как А(2![]() 3), В(3
3), В(3![]() 3), то АВ(2
3), то АВ(2![]() 3) и
3) и
АВ=![]()
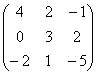 .=
.=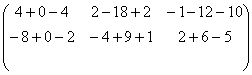 =
=![]() .
. ![]()
3)Найти А3, если А=![]() .
.
![]() Возведение в третью степень матрицы А означает умножение ее трижды на саму себя, то есть А3=ААА.
Возведение в третью степень матрицы А означает умножение ее трижды на саму себя, то есть А3=ААА.
Вначале найдем А2:
AA=![]()
![]() =
=![]() .
.
Теперь А3=А2А=![]()
![]() =
=![]() .
. ![]()
4)Найти АВС, если
А=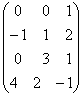 , B=
, B=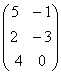 , C=
, C=![]() .
.
![]() В силу свойства ассоциативности матриц: АВС=(АВ)С=А(ВС).
В силу свойства ассоциативности матриц: АВС=(АВ)С=А(ВС).
Выбор последовательности умножения матриц зависит от простоты вычислений. Так, если вначале умножать матрицу А(4![]() 3) на В(3
3) на В(3![]() 2), то образуется матрица АВ размера (4
2), то образуется матрица АВ размера (4![]() 2), а если перемножать В (3
2), а если перемножать В (3![]() 2) и С(2
2) и С(2![]() 1), то получится матрица ВС размера (3
1), то получится матрица ВС размера (3![]() 1) и содержащая меньше искомых элементов, чем АВ.
1) и содержащая меньше искомых элементов, чем АВ.
Находим ВС:
BC=
![]() =
=![]() .
.
Теперь АВС=А(ВС)=
=
![]() =
=![]() .
. ![]()
5)Дана матрица А:
A= .
.
Найти обратную матрицу ![]() .
.
![]() Вычислим определитель матрицы А, разложив его по второй строке:
Вычислим определитель матрицы А, разложив его по второй строке:
det(A)= =-3
=-3![]() -2
-2![]() =-4.
=-4.
Так как det(A)¹0, то по теореме об обратной матрице, ![]() определена.
определена.
Найдем алгебраические дополнения соответствующих элементов определителя det(A):
| A11= |
A21=- |
A31= |
| A12=- |
A22= |
A32=- |
| A13= |
A23=- |
A33= |
Строим союзную матрицу ![]() :
:
![]() =
=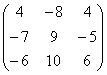 .
.
Следовательно, ![]() =
=![]()
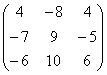 =
=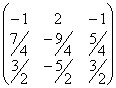 .
. ![]()
6)Найти ранг и базисные миноры матрицы А:
1. A= ,
,
2. A=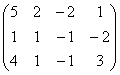 .
.
![]() 1.Вычеркнув из матрицы А нулевые второй, третий столбец и вторую строку, получим матрицу, эквивалентную заданной:
1.Вычеркнув из матрицы А нулевые второй, третий столбец и вторую строку, получим матрицу, эквивалентную заданной:
A~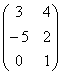 . Так как
. Так как ![]() =26¹0, то ранг исходной матрицы равен 2.
=26¹0, то ранг исходной матрицы равен 2.
Базисными минорами исходной матрицы являются миноры второго порядка, отличные от нуля:
![]() ,
, ![]() ,
, ![]() .
.
2.Производя последовательно элементарные преобразования, будем иметь:
A~C3+C2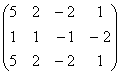 ~C1-C3
~C1-C3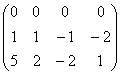 ~
~![]()
 .
.
Вычеркнем нулевые первую строку и второй столбец и продолжим преобразования:
A~![]() ~C2-5C1
~C2-5C1![]()
![]() .
.
Ранг последней матрицы равен 2, так как, например, ![]() =3¹0.
=3¹0.
Следовательно, ранг исходной матрицы равен 2, а базисные миноры имеют второй порядок:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]()
7)Выяснить, является ли система арифметических векторов линейно зависимой или линейно не зависимой.
1. ![]() {-3 1 5 2},
{-3 1 5 2}, ![]() {-6 2 10 4},
{-6 2 10 4},
2. ![]() {2 –3 1},
{2 –3 1}, ![]() {3 –1 5},
{3 –1 5},![]() {1 –4 3},
{1 –4 3},
3. {0 1 1 -1}, ![]() {1 2 0 1},
{1 2 0 1},![]() {2 3 –1 3},
{2 3 –1 3},![]() {-1 0 2 –3}.
{-1 0 2 –3}.
![]() 1. Замечаем, что
1. Замечаем, что ![]() =2
=2![]() . Отсюда имеем, что линейная комбинация l1
. Отсюда имеем, что линейная комбинация l1![]() +l2
+l2![]() =0, если l1=2, l2=-1. Следовательно, вектора
=0, если l1=2, l2=-1. Следовательно, вектора ![]() и
и ![]() линейно зависимы по определению.
линейно зависимы по определению.
Случаи 2. и 3. не являются тривиальными, и для их изучения будем использовать критерий линейной зависимости (независимости) векторов: Система векторов линейно зависима (независима) тогда и только тогда, когда ранг матрицы А, составленной из элементов данной системы векторов, меньше (соответственно равен) числа векторов системы.
2.Составим матрицу А, элементарными преобразованиями приведем ее к ступенчатому виду и подсчитаем ранг:
A=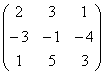 ~C2+C1
~C2+C1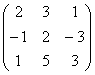 ~C3+C2
~C3+C2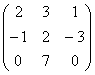 ~C1+2C2
~C1+2C2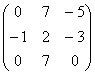 ~C1«C2
~C1«C2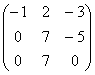 ~
~![]()
 .
.
Ранг матрицы А равен трем, поскольку минор  =35
=35![]() 0. Число векторов системы совпадает с рангом, следовательно, исходная система линейно независима.
0. Число векторов системы совпадает с рангом, следовательно, исходная система линейно независима.
3.Аналогично предыдущему, составим и преобразуем матрицу А:
A= ~C1-C4 , C3-C2
~C1-C4 , C3-C2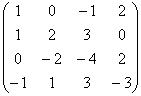 ~C2-C1, C4+C1
~C2-C1, C4+C1 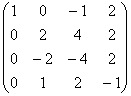 ~ ~C3+C2
~ ~C3+C2  ~C4-0,5C2
~C4-0,5C2 ~C3+2C4
~C3+2C4 ~ ~
~ ~ ~
~ .
.
Ранг матрицы А равен 3, так как, например, минор
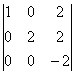 =-4¹0.
=-4¹0.
Число векторов системы равно 4 и не совпадает с рангом, следовательно, исходная система линейно зависима. ![]()