Лекция 3. Кривые второго порядка.

Порядком алгебраического уравнения называется высшая степень входящего в уравнение неизвестного. Порядок кривой не зависит от выбора осей координат на плоскости.

Общий вид кривой 2-го порядка:

а₁₁х² + 2а₁₂хy + а₂₂y² + 2а₁₃х + 2а₂₃y + а₃₃ = 0 (1)

К кривым 2-го порядка относятся эллипс, частным случаем которого является окружность, гипербола и парабола.

1. Окружность

Пусть с(а;b) – центр окружности радиуса R, тогда уравнение окружности имеет вид:

(х – а)² + (y –b)²= R² (2)

если сравнить уравнение окружности (2) с общим уравнением кривой 2-го порядка, то нетрудно заметить, что для уравнения окружности выполняются условия: коэффициенты при квадратах неизвестных равны между собой, а член с произведением координат отсутствует, то есть a₁₁=a₂₂, a₁₂=0.

2. Эллипс (в декартовой системе координат)

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данный точек, называемых фокусами эллипса, постоянна и равна 2а.

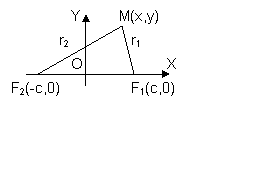
Пусть фокусами эллипса являются точки F₁ и F₂, при этом F₁ F₂ = 2с есть фокальная ось эллипса. М – некоторая точка, принадлежащая эллипсу. По определению эллипса, для любой его точки М, имеем:

МF₁ + MF₂ = 2а

Пусть ось OX совпадает с фокальной осью F₁ F₂ . Начало координат выберем посередине между F₁ и F_2., а ось OY перпендикулярно фокальной оси. При таком выборе системы координат уравнение эллипса примет вид:

Так как из ∆ F₁МF₂ следует , что 2а > 2с т.е. а>с, то полагают а² – с²= в² и получают каноническую (простейшую) форму уравнения эллипса:

Эксцентриситет эллипса e=<1.

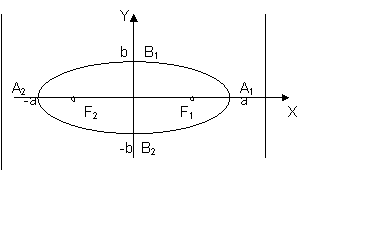
А₁, А_2,В₁, В₂ – вершины эллипса, a директрисы имеют уравнения x= .

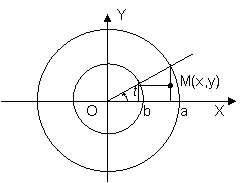
Параметрические уравнения эллипса

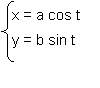
3. Гипербола

Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами гиперболы, постоянна и равна ±2а.

Фокальная ось гиперболы F₂ F₁ = 2а; r₁ r₂ – фокальные радиусы гиперболы,

соответствующие точке М(х,у). r₂– r₁ = ± 2а; 2с > 2а. с>а ( по свойству сторон треугольника)

Каноническое уравнение гиперболы

Обозначим с²-a²=b², тогда уравнение гиперболы примет вид:

Вершины гиперболы: А₁(а;о) А₂(-а,о) – вещественные вершины; В₁(о;в) В₂(о;-в) – мнимые вершины.

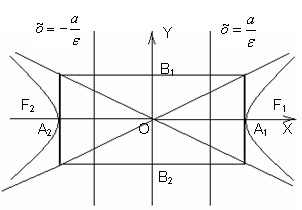
Прямые y=являются асимптотами гиперболы.

Гипербола состоит из двух несмыкающихся ветвей, лежащих в углах между прямыми у =, y= и неограниченно приближающихся к этим прямым. А₁ вещественная ось, В₁В₂ – мнимая ось.

Эксцентриситет гиперболы e=>1.

Директрисы гиперболы обладают тем свойством, что отношение расстояния любой точки гиперболы до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы.

Уравнение директрис х = или х =.

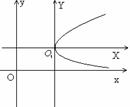
4. Парабола

Параболой называется множество точек плоскости, одинаково удаленных от заданной прямой (директрисы) и заданной точки (фокуса)

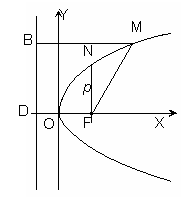
Пусть точка F(, 0) – фокус. Прямая BD – директриса параболы ;

М(х,у) – произвольная точка параболы, FD = Р >0 параметр параболы.

По определению параболы МF = МВ. Уравнение параболы с вершиной в точке 0(0;0) и директрисой BD, заданной уравнением х = , имеет канонический вид:

1) у² = 2 ρх .

Замечание: если положить х = , то y=p, то есть NF=p (NFOX).

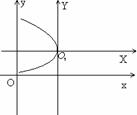
Другие виды параболы:

2) у² = - 2 ρх - парабола с осью симметрии OХ, фокусом F(-, 0) и директрисой x=.

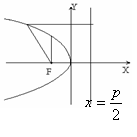
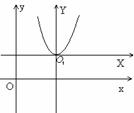
3)

X

х² = 2 ρу- парабола с осью симметрии OY, фокусом F(0, ) и директрисой y= -.

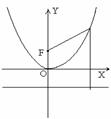
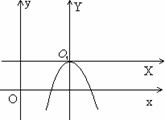
4) х²= -2 ρу- парабола с осью симметрии OY, фокусом F(0,-) и директрисой y=.

Преобразование координат.

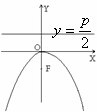
1.Параллельный перенос.

Изменяется начало координат, а направление осей и масштаб остаются неизменны.

, ^’{X,Y}, {x, y}, =₁+₀, тогда

или

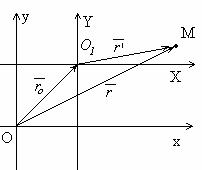
- формулы преобразования координат при параллельном переносе осей координат

2.Поворот осей координат.

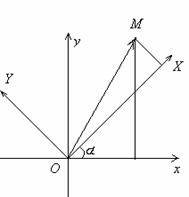
Пусть М(х;у) в системе xoy, M(X,Y) в системе XOY.

Тогда формулы перехода при повороте осей координат на угол a

к системе хоу имеют вид:

а к системе XOY:.

Кривые 2-го порядка с осями симметрии, параллельными осям

координат.

1.Эллипс.

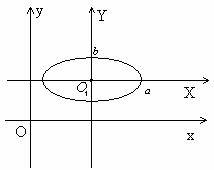
Уравнение эллипса в системе XOY: .

Уравнение эллипса со смещенным в точку О₁(m,n) центром:

Возможны случаи вырождения эллипса в точку, например,

- точка O₁ (m,n), или мнимый эллипс:.

2.Гипербала.

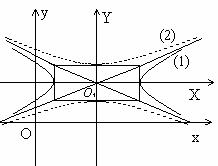
Уравнение гиперболы с центром в точке О₁(m,n): , (1).

Уравнение гиперболы, вырожденной в свои асимптоты,

имеет вид: .

Уравнение гиперболы, сопряженной к данной: , (2).

3. Парабола.

Парабола с вершиной в точке О₁(m,n), с осью симметрии параллельной ОХ, р>0.

Парабола с вершиной в точке О₁(m,n), с осью симметрии параллельной ОХ.

Парабола с вершиной в точке О₁(m,n), с осью симметрии параллельной ОY.

Если сравнить уравнения кривых 2-го порядка с осями симметрии, параллельными осям координат с общим уравнением кривой второго порядка, то очевидно, всюду коэффициент с произведением координат отсутствует, т.е. а₁₂ = 0 и

1)если кривая эллиптического типа, то а₁₁ а₂₂ >0

2)если кривая гиперболического типа, то а₁₁ а₂₂ <0

3)если кривая параболического типа (парабола или ее вырождения в пару параллельных прямых или пару слившихся прямых), то выполняется условие а₁₁ а₂₂ = 0.

Полярная система координат.

При решении многих задач аналитической геометрии оказывается более удобным определять положение точки на плоскости не прямоугольными декартовыми координатами, а так называемыми полярными координатами.

Система полярных координат задается полюсом - точкой О и полупрямой, исходящей из полюса («луч»- - полярная ось).

ОМ = ρ, МОρ =j. Числа ρ и j определяют положение точки М относительно системы координат, их называют полярными координатами точки М(ρ;j).

Чтобы установить взаимнооднозначное соответствие между точками плоскости и координатами этой точки, ограничим изменение полярного угла промежутком -p<j£p (или иным промежутком длины 2π). Значения , удовлетворяющие этому условию, называют главными значениями. Назовем полярные координаты ρ, j основными, если ρ ≥0, а j есть главное значение полярного угла, т.е. если -p<j£p .

Связь между прямоугольными и полярными координатами.

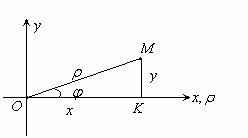
Пусть полюс системы координат совпадает с началом декартовой системы координат, а полярная ось совпадает с положительной полуосью OX. Тогда из _ΔОМК : - это формулы перехода к декартовой системе координат.

Выведем формулы обратного перехода от декартовых координат к полярным.

Полярный радиус – вектор ρ, будучи расстоянием от точки М до начала координат, будет равен

, а также, , .

Угол определяется из условия: tgj = и знаков функций .

Пример.

Найти полярные координаты точки А(3;-4).

r=, , , tgj =. Так как угол j находится в IV четверти, то j= - arctg . Отсюда, A(5, - arctg ), или А(5;-53 ⁰).

Полярные уравнения кривых второго порядка.

Кривая второго порядка – это множество точек плоскости, для каждой их которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету (е).

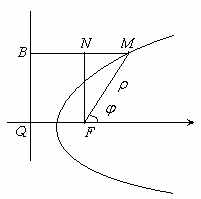
Пусть F – фокус кривой, BQ отвечающая этому фокусу директриса, FQ =p, пусть полюс полярной системы координат совпадает с F, а полярная ось перпендикулярна BQ и направлена как указано на рисунке.

Пусть M – любая точка кривой. Тогда, согласно определению кривой, 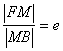. Так как , , то , откуда .

При этом: - окружность; 0< e <1 – эллипс; e = 1 – парабола; e >1 – гипербола.

Примеры на тему: ”Кривые второго порядка”.

Пример 1. Установить, что уравнение 5x²+9y²-30x+18y+9=0 определяет эллипс. Найти его центр С, полуоси, координаты фокусов F₁, F₂, эксцентриситет и уравнения директрис. Сделать чертеж.

Решение: 1. В заданном уравнении сгруппируем слагаемые, содержащие одноименные координаты и вынесем коэффициенты при квадратах за скобки:

5(x²-6x)+9(y²+2y)+9=0.

Дополним выражения, стоящие в скобках, до полного квадрата и полученные свободные константы перенесем в правую часть:

5(x²-6x+9-9)+9(y²+2y+1-1)+9=0,

5((x-3)²-9)+((y+1)²-1)+9=0,

5(x-3)²+9(y+1)²=45.

Разделим обе части уравнения на 45, получим

2. Введем новую систему координат XOY, полученную сдвигом по каждой из координатных осей, и связанную со старой декартовой системой координат равенствами:

(1).

Тогда, исследуемое уравнение кривой относительно новых осей примет вид:

, .

Это есть канонический вид эллипса с центром (0,0), большой полуосью a=3, малой полуосью b=. Фокусы эллипса располагаются на оси OX на расстоянии с=от начала координат О, в точках ₁(с, 0), ₂(-c, 0) в новой системе координат XOY.

Вычисляем, с===2, ₁(2, 0), ₂(-2, 0). Мера сжатия, то есть эксцентриситет, дается равенством e=. Отсюда e=.Директрисы эллипса в системе XOY задаются уравнениями X=. В нашем случае, X=.

3. Чтобы найти координаты центра и фокусов в старой системе xoy, воспользуемся равенствами (1), осуществляющими связь систем координат:

центр С: , C(3, -1),

фокусы F₁ :_,F₁(5,-1), F₂: , F₂(1,-1).

Уравнения директрис: x-3=.

4. Теперь построим эллипс. С помощью параллельного переноса системы координат xoy образуем новую систему

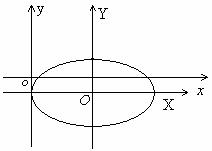
координат XOY так, чтобы новое начало координат О совпадало с точкой С(3, -1). При указанном выборе, оси координат системы XOY являются осями симметрии эллипса, а точка О- центром симметрии. Теперь симметрично О по оси OX отложим отрезки длины a=3, а по оси OY отрезки длины . Соединив найденные вершины, получим эллипс. На оси OX симметрично относительно О на расстоянии с=2 отложим точки F₁, F₂-фокусы эллипса. Так как директрисы эллипса описываются уравнениями x=const, то они располагаются параллельно OY, причем одна из них проходит через

точку (7,5 ; 0), другая через (-1,5; 0).

Пример 2. Установить, что уравнение 16x²-9y²-64x-54y-161=0 определяет гиперболу. Найти ее центр С, полуоси, координаты фокусов F₁, F₂, вершины А_1, А₂ , эксцентриситет , уравнения директрис и асимптот. Сделать чертеж.

Решение: 1. В уравнении линии выделим полные квадраты при одноименных переменных:

16(x-2)²-9(y+3)²=144.

Разделив обе части уравнения на 144, будем иметь:

2. Введем новую систему координат XOY, полученную сдвигом по каждой из координатных осей и связанную с xoy равенствами:

(2).

В этой системе исследуемое уравнение представляет собой каноническое уравнение гиперболы:

с центром в точке (0,0), большой полуосью b=4 и малой a=3. Точки ₁(с, 0), ₂(-c, 0), где с=являются фокусами гиперболы, отсюда находим с==5, ₁(5, 0), ₂(-5, 0). Эксцентриситет

e=, в нашем случае e=. Вершины гиперболы располагаются по оси OX симметрично относительно начала координат и на расстоянии a=3 от центра, поэтому ₁(3, 0), ₂(-3, 0). По формулам асимптот и директрис:

Y=X и X=, найдем

Y=X - уравнения асимптот, X=-уравнения директрис.

3. Вернемся к исходной системе координат xoy, воспользовавшись равенствами (2):

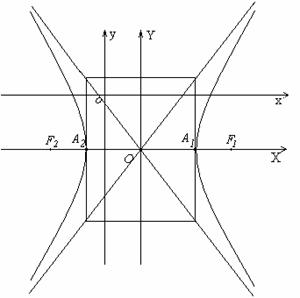
C(2;-3), F₁(7;-3), F₂(-3; -3), A₁(5; -3), A₂(-1; -3), асимптоты: y+3=(x-2), директрисы: x-2=.

4. Теперь построим гиперболу. С помощью параллельного переноса системы координат xoy образуем новую систему координат XOY так, чтобы новое начало координат О совпадало с точкой С(2, -3). При указанном выборе, оси координат системы XOY являются осями симметрии гиперболы, а точка О- центром симметрии.

Теперь симметрично О по оси OX отложим отрезки длины a=3, а по оси OY отрезки длины b=4, образуем основной прямоугольник гиперболы. При пересечении основного прямоугольника с осью OX образуются вершины А₁, А₂. Через противоположные вершины основного прямоугольника проведем прямые, которые будут являться асимптотами гиперболы. Теперь проводя через вершины и приближаясь к асимптотам,

рисуем ветви гиперболы. F₁, F₂-фокусы гиперболы располагаются по оси абсцисс OX симметрично начала координат О на расстоянии с=5.

Пример 3. Установить, что уравнение x=-2y²+12y-14 определяет параболу, найти ее вершину, параметр, фокус, директрису. Сделать чертеж.

Решение: 1. В заданном уравнении сгруппируем слагаемые содержащие переменную y, вынесем коэффициент при квадрате за скобку и выделим полный квадрат:

x= -2(y-3)²+4, x – 4= -2(y-3)².

2. Введем новую систему координат XOY, связанную со старой , следующими формулами:

, (3)

тогда исследуемое уравнение относительно новых осей примет вид:

X= -2Y², Y²= - X.

Полученное уравнение представляет собой каноническую форму уравнения параболы, симметричной относительно оси OX, с ветками, направленными в отрицательную сторону OX, и вершиной в точке (0; 0). Константа перед X, есть величина 2p, поэтому 2p= , а параметр p=. Фокус и уравнение директрисы при таком расположении параболы находятся по формулам , X=, отсюда имеем фокус , директриса X=.

3. Вернемся к исходной системе координат xoy. Используя равенства (3), получаем: A(4;3), F(3; 3), директриса x=4.

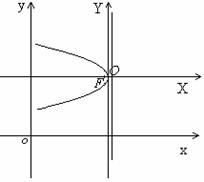
4. Построение параболы. С помощью параллельного переноса системы координат xoy так, чтобы новое начало координат О совпадало с точкой А(4; 3), образуем новую систему XOY.

Рисуем параболу с вершиной в точке А=О и обладающую перечисленными выше свойствами.

Фокус параболы лежит на расстоянии = от вершины. Директриса параболы проходит через точку (4; 0) параллельно OY.

В начало

Оглавление

На главную