Лекция 2. Линейные образы в R3 .
Пусть в пространстве задана декартова прямоугольная система координат. Рассмотрим сферу радиуса R, с центром в точке А(а,в,с). Сфера- множество точек, отстоящих от центра на одном и том же расстоянии R. Обозначим через M(x,y,z) произвольную точку на сфере, радиуса R, тогда ![]() . Мы получим две точки:
. Мы получим две точки:
![]() (1).
(1).
Возведя в квадрат обе части равенства (1), мы получим более удобную формулу:
![]()
![]() (2).
(2).
Равенство (2) называется уравнением сферы с центром в точке А(а,в,с) и радиуса R.
Определим теперь, что следует вообще понимать под уравнением некоторого множества. Пусть выбрана система координат. Под уравнением множества S в этой системе координат мы будем понимать выражение определения S через координаты его точек, т.е. высказывание, верное для координат точек, принадлежащих S, и неверное для координат точек, ему не принадлежащих.
Понятие алгебраической поверхности.
Определение. Алгебраической поверхностью называется множество, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида:![]() (3),
(3),
где все показатели степени – целые неотрицательные числа. Наибольшая из сумм: ![]() называется степенью уравнения, а также периодом алгебраической поверхности. Это определение означает, в частности, что сфера, уравнение которой в прямоугольной системе координат имеет вид (2), является алгебраической поверхностью второго порядка.
называется степенью уравнения, а также периодом алгебраической поверхности. Это определение означает, в частности, что сфера, уравнение которой в прямоугольной системе координат имеет вид (2), является алгебраической поверхностью второго порядка.
Перейдем к рассмотрению линейных образов в пространстве R3.
Плоскость.
1.Уравнение плоскости ![]() , проходящей через данную точку М0(x0,y0,z0), перпендикулярно данному вектору
, проходящей через данную точку М0(x0,y0,z0), перпендикулярно данному вектору ![]() .
.

М(x,y,z)- текущая точка плоскости ![]() . Вектор
. Вектор ![]() . Для любой точки плоскости векторы
. Для любой точки плоскости векторы ![]() и
и ![]() ортогональны, следовательно, их скалярное произведение равно 0.
ортогональны, следовательно, их скалярное произведение равно 0. ![]() . (4)
. (4)
В уравнении (4) перейдём к координатной форме:
![]() . (5)
. (5)
Уравнение (5) называется уравнением плоскости, проходящей через данную точку, перпендикулярно данному вектору.
2. Общее уравнение плоскости- это уравнение 1-ой степени с неизвестными x,y,z имеет вид: Ax+By+Cz=0. (6)
3. Уравнение плоскости, проходящей через три данные точки.
Пусть плоскости ![]() принадлежат точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3),
принадлежат точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3),

M(x,y,z) - текущая точка плоскости, тогда векторы ![]() ,
,
![]() ,
,
![]() компланарны и, следовательно, смешанное произведение этих векторов равно нулю.
компланарны и, следовательно, смешанное произведение этих векторов равно нулю.
![]() , или
, или 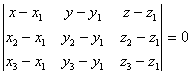 . (7)
. (7)
4. Уравнение плоскости «в отрезках»:
![]() , где а,b,с – величины отрезков, отсекаемых плоскостью от начала координат на осях координат.
, где а,b,с – величины отрезков, отсекаемых плоскостью от начала координат на осях координат.
5. Расстояние точки от плоскости.
Дана плоскость ![]()
![]() и точка
и точка ![]() вне плоскости, тогда расстояние
вне плоскости, тогда расстояние ![]() точки M0 от плоскости
точки M0 от плоскости ![]() имеет вид:
имеет вид:
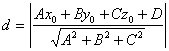
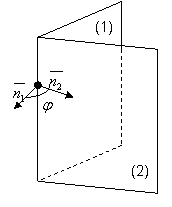
6. Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей.
Даны две плоскости:
![]() (1)
(1)
![]() (2)
(2)
и ![]() ;
; ![]() - нормальные векторы к соответствующим данным плоскостям.
- нормальные векторы к соответствующим данным плоскостям.
За угол между двумя плоскостями принимается угол между их нормальными векторами:
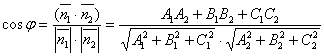 .Если плоскости параллельны, то векторы
.Если плоскости параллельны, то векторы ![]() и
и ![]() коллинеарны, и, следовательно,
коллинеарны, и, следовательно,
![]() - условие параллельности двух плоскостей.
- условие параллельности двух плоскостей.
Если плоскости перпендикулярны, то ![]() - условие перпендикулярности двух плоскостей.
- условие перпендикулярности двух плоскостей.
Прямая линяя в пространстве.
Линия в пространстве определяется как пересечение двух поверхностей, то есть задается совокупностью двух уравнений:
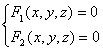 .
.
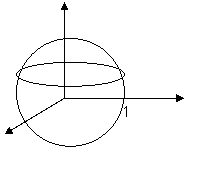
Например:
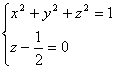 - окружность в плоскости z=
- окружность в плоскости z=![]()
Прямую линию в пространстве можно представить как пересечение двух плоскостей, то есть совокупность двух уравнений плоскостей. Систему двух непараллельных уравнений называют общими уравнениями прямой:
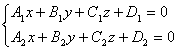 .
.
Канонические уравнения прямой в пространстве.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором данной прямой и обозначается: ![]() {m,n,p}.
{m,n,p}.
Если известна точка М0(x0, y0, z0), прямой и направляющий вектор ![]() {m,n,p}, то прямая может быть определена (двумя) уравнениями вида:
{m,n,p}, то прямая может быть определена (двумя) уравнениями вида:
![]() , (1)
, (1)
которые называются каноническими уравнениями прямой.
Канонические уравнения прямой, проходящей через две данные точки М0(x0, y0, z0), M1 (x 1 ,y1, z1) имеют вид:
![]() . (2)
. (2)
Обозначив буквой t каждое из равных отношений в канонических уравнениях, мы получим
![]() = t, отсюда
= t, отсюда 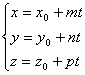 . (3)
. (3)
Уравнения (3) есть параметрические уравнения прямой, проходящей через точку М0(x0,y0, z0), параллельно вектору ![]() {m,n,p}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр; x, y, z - как функции от t. При изменении t величины x, y, z меняются так, что точка М(x,y,z) движется по данной прямой.
{m,n,p}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр; x, y, z - как функции от t. При изменении t величины x, y, z меняются так, что точка М(x,y,z) движется по данной прямой.
Приведение общих уравнений прямой к каноническому виду.
Пусть прямая задана общими уравнениями:
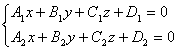 , (1)
, (1)
где ![]() 1{A 1,B1,C1},
1{A 1,B1,C1}, ![]() 2{A2, B2, C2} – нормальные векторы заданных плоскостей .
2{A2, B2, C2} – нормальные векторы заданных плоскостей .
Выберем на прямой определенную точку М0(x0, y0, z0). Для этого, например, z0 зададим произвольно, а x0 и y0 получим из системы (1).
В качестве направляющего вектора возьмем вектор ![]() :
:
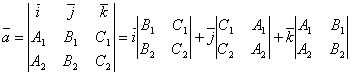 .
.
Следовательно, канонические уравнения прямой, соответствующие системе (1), имеют вид:
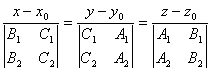 .
.
Угол между двумя прямыми.
За угол между двумя прямыми
![]() ,
, ![]() ,
,
принимается угол между их направляющими векторами.
Здесь ![]() ={m1,n1,p1},
={m1,n1,p1}, ![]() {m2,n2,p2} – направляющие вектора данных прямых, cosj=
{m2,n2,p2} – направляющие вектора данных прямых, cosj=![]() . Условие параллельности двух прямых:
. Условие параллельности двух прямых: ![]() .
.
Условие перпендикулярности двух прямых: m1m2 + n1n2 + p1p2=0.
Задачи на тему “Прямая в пространстве”.
1) Составить каноническое уравнение прямой L, проходящей через две заданные точки А(1 –2 1), В(3 1 -1).
2) ![]() На прямой L возьмем произвольным образом точку М(x y z) и соединим ее с какой-либо известной точкой на этой прямой, например, точкой А. Образуем текущий вектор
На прямой L возьмем произвольным образом точку М(x y z) и соединим ее с какой-либо известной точкой на этой прямой, например, точкой А. Образуем текущий вектор ![]() {x-1 y+2 z-1}. Вектор
{x-1 y+2 z-1}. Вектор ![]() {2 3 -2}, лежащий на прямой L, является направляющим вектором для L.
{2 3 -2}, лежащий на прямой L, является направляющим вектором для L.
Для любой точки М(x y z)![]() L вектора
L вектора ![]() II
II![]() , следовательно, условие параллельности векторов описывает уравнение прямой L:
, следовательно, условие параллельности векторов описывает уравнение прямой L:
![]() .
. ![]()
3) Составить уравнение прямой![]() , проходящей через точку А(1 –1 2), параллельно прямой
, проходящей через точку А(1 –1 2), параллельно прямой ![]() :
:
![]()
![]() На прямой
На прямой ![]() образуем текущий вектор
образуем текущий вектор ![]() {x-1 y+1 z-2}. Из канонического уравнения прямой
{x-1 y+1 z-2}. Из канонического уравнения прямой ![]() находим направляющий вектор
находим направляющий вектор![]() {5 –2 0}, здесь m=5, n=-2, p=0. Так как
{5 –2 0}, здесь m=5, n=-2, p=0. Так как ![]() II
II![]() , то
, то ![]() II
II![]() для любой точки М(x y z)
для любой точки М(x y z)![]()
![]() . Используя теперь условие параллельности, получаем каноническое уравнение прямой
. Используя теперь условие параллельности, получаем каноническое уравнение прямой ![]() :
:
![]() .
. ![]()
4) Известны уравнения двух прямых:
![]() :
: ![]() ,
,![]() :
:![]()
a) Проверить, являются ли ![]() и
и ![]() параллельными.
параллельными.
b) Проверить, являются ли ![]() и
и ![]() перпендикулярными.
перпендикулярными.
c) Найти угол ![]() между
между ![]() и
и ![]() .
.
![]() а) Из условия параллельности прямых имеем,
а) Из условия параллельности прямых имеем, ![]() II
II![]() , если их направляющие вектора
, если их направляющие вектора ![]() и
и ![]() параллельны. Координаты вектора
параллельны. Координаты вектора ![]() легко получаются из заданного канонического уравнения прямой
легко получаются из заданного канонического уравнения прямой ![]() :
: ![]() {-1 3 1}. Для прямой
{-1 3 1}. Для прямой ![]() , определяемой пересечением плоскостей, направляющий вектор
, определяемой пересечением плоскостей, направляющий вектор ![]() находится как векторное произведение:
находится как векторное произведение: ![]() =
=![]() , где
, где ![]() {1 –1 0},
{1 –1 0}, ![]() {2 1 -5}. Вычисляем,
{2 1 -5}. Вычисляем,
![]() =
=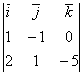 =5
=5![]() +5
+5![]() +3
+3![]() ,
, ![]() {5 5 3}.
{5 5 3}.
Так как координаты векторов ![]() и
и ![]() не пропорциональны, то условие параллельности для векторов
не пропорциональны, то условие параллельности для векторов ![]() и
и ![]() не выполняется, а значит
не выполняется, а значит ![]() не параллельна
не параллельна ![]() .
.
b) Из условия перпендикулярности прямых, ![]()
![]()
![]() , если
, если ![]()
![]()
![]() . Так как
. Так как ![]() =13, то условие перпендикулярности векторов
=13, то условие перпендикулярности векторов ![]() и
и ![]() не выполняется. Стало быть,
не выполняется. Стало быть, ![]() не перпендикулярна к
не перпендикулярна к ![]() .
. ![]()
c) Угол между прямыми найдем по формуле:
cos![]() =соs(
=соs(![]()
![]() ,
,![]() )=
)=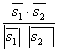 .
.
Отсюда, соs![]() =
=![]() .
. ![]()
5) Привести к каноническому виду уравнение прямой:
![]() .
.
![]() Найдем направляющий вектор прямой
Найдем направляющий вектор прямой ![]() :
:
![]() =
=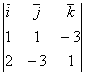 =-8
=-8![]() -7
-7![]() -5
-5![]() ,
, ![]() {-8 –7 -5}.
{-8 –7 -5}.
За точку М0(x0 y0 zo), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью YOZ. Так как при этом x0=0, то координаты y0,z0 определяются из заданного уравнения прямой, если в нем положить x=0:
![]() .
.
Откуда находим z0=![]() , y0=
, y0=![]() и M0(0
и M0(0 ![]()
![]() ).
).
Итак, воспользовавшись теперь общей формулой канонического уравнения прямой, получаем:
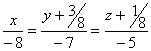 .
. ![]()
Прямая и плоскость.
1) Угол между прямой и плоскостью.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.
Пусть даны плоскость (a) : Ax+By+Cz+D=0 c нормальным вектором ![]() {A,B,C} и прямая
{A,B,C} и прямая
![]() с направляющим вектором
с направляющим вектором ![]() {m,n,p}.
{m,n,p}.
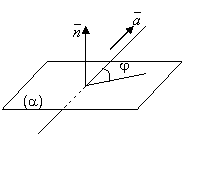
Угол между векторами ![]() и
и ![]() отличается от угла между прямой и плоскостью на
отличается от угла между прямой и плоскостью на ![]() ;
;
Cos(![]() )=
)=![]() , или sinj=
, или sinj=![]() .
.
2) Условие параллельности прямой и плоскости:
Am+Bn+Cp=0.
3) Условие перпендикулярности прямой и плоскости:
![]() .
.
Условие того, что прямая лежит в данной плоскости.
Пусть Ax+By+Cz+D=0 данная плоскость (a),
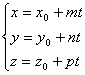 (1)-параметрическое уравнение прямой, проходящей через точку М0(x0,y0, z0), параллельно вектору
(1)-параметрическое уравнение прямой, проходящей через точку М0(x0,y0, z0), параллельно вектору ![]() {m,n,p}.
{m,n,p}.
Условие принадлежности прямой (1) плоскости (a) имеет вид:
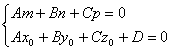 .
.
Если прямая лежит в плоскости, то она этой плоскости параллельна и любая точка прямой удовлетворяет уравнению плоскости.
Условие того, что две прямые лежат в одной плоскости.
Пусть имеем две прямые:
![]() и
и ![]() .
.
Отсюда, направляющие вектора этих прямых ![]() 1{m1, n1, p1}.
1{m1, n1, p1}. ![]() 2{m2, n2, p2} и точки М1(x1,y1,z1), M2(x2, y2, z2) на соответствующих прямых. Если прямые лежат в одной плоскости, то векторы
2{m2, n2, p2} и точки М1(x1,y1,z1), M2(x2, y2, z2) на соответствующих прямых. Если прямые лежат в одной плоскости, то векторы ![]()
![]() и
и ![]() 2 компланарны. Условие того, что две прямые лежат в одной плоскости равносильно условию компланарности этих векторов: (
2 компланарны. Условие того, что две прямые лежат в одной плоскости равносильно условию компланарности этих векторов: (![]() )=0 или
)=0 или 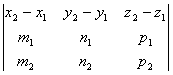 =0. (2)
=0. (2)
Условие (2) является также критерием пересечения двух прямых.
Замечание. Если заданы две прямые, то они могут быть в одном из трех следующих соотношений:
1) параллельны, ![]()
![]()
![]() ,
,
2) пересекаются, ![]()
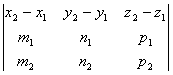 =0
=0
3) прямые (1) и (2) скрещиваются, следовательно, (![]() )¹0. Тогда возникает вопрос об определении расстояния между скрещивающимися прямыми, как высоты параллелепипеда, построенного на векторах
)¹0. Тогда возникает вопрос об определении расстояния между скрещивающимися прямыми, как высоты параллелепипеда, построенного на векторах

![]() , как на сторонах:
, как на сторонах:
![]() d=
d=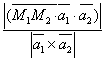 .
.
Смешанные задачи на прямую и плоскость.
1) Найти уравнение плоскости, проходящей через точку А(1 –2 3) параллельно прямым
L1: ![]() и L2:
и L2: 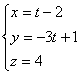 .
.
![]() На искомой плоскости образуем текущий вектор
На искомой плоскости образуем текущий вектор ![]() {x-1 y+2 z-3}. Из канонического уравнения прямой L1 и параметрического уравнения прямой L2 получим координаты их направляющих векторов
{x-1 y+2 z-3}. Из канонического уравнения прямой L1 и параметрического уравнения прямой L2 получим координаты их направляющих векторов ![]() {3 4 -1} и
{3 4 -1} и ![]() {1 –3 0}. Так как
{1 –3 0}. Так как ![]() II L1,
II L1, ![]() II L2 и L1IIα, L2IIα, то
II L2 и L1IIα, L2IIα, то ![]() IIα,
IIα, ![]() IIα. Поскольку с векторами в пространстве можно совершать параллельный перенос, то можно считать, что
IIα. Поскольку с векторами в пространстве можно совершать параллельный перенос, то можно считать, что ![]()
![]() α,
α, ![]()
![]() α.
α.
Так как ![]() не параллелен
не параллелен ![]() , и для любой точки М(x y z) три вектора
, и для любой точки М(x y z) три вектора ![]() ,
,![]() ,
,![]() лежат в плоскости α, то условие (
лежат в плоскости α, то условие (![]() ,
,![]() ,
,![]() )=0 дает уравнение плоскости α:
)=0 дает уравнение плоскости α:
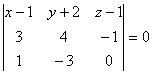 .
. ![]()
2) Найти уравнение плоскости, проходящей через точку А(-2 1 0) и прямую L:
![]() .
.
![]() На искомой плоскости образуем текущий вектор
На искомой плоскости образуем текущий вектор ![]() {x+2 y-1 z}.
{x+2 y-1 z}.
Уравнение прямой задано пересечением плоскостей, поэтому ее направляющий вектор ![]() определяется из равенств:
определяется из равенств:
![]() =
=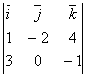 =2
=2![]() +13
+13![]() +6
+6![]() ,
, ![]() {2 13 6 }.
{2 13 6 }.
Так как ![]() II L, L
II L, L![]() , то
, то ![]()
![]() .
.
На прямой L зафиксируем произвольную точку В. Координаты В найдем из системы уравнений заданной прямой, положив в них, например, X=0:
![]() .
.
Решая эту систему, получим Y=4,5 ,Z=2. Таким образом, В(0 4,5 2). Соединив точки А и В, получим вектор ![]() {2 3,5 2}, принадлежащий плоскости α.
{2 3,5 2}, принадлежащий плоскости α.
Для любой точки М(x y z) ![]() выполняется условие компланарности векторов (
выполняется условие компланарности векторов (![]() ,
,![]() ,
,![]() )=0 и так как
)=0 и так как
![]() не параллелен
не параллелен ![]() , то уравнение плоскости дается равенством:
, то уравнение плоскости дается равенством:
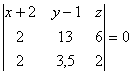
![]()
3) Найти уравнение плоскости α, проходящей через прямые
L1: ![]() и L2:
и L2: ![]() .
.
![]() Из канонического уравнения прямой L1 найдем координаты некоторой точки А, расположенной на L1: А(1 0 -2) и, соединив ее с текущей точкой М(x y z), образуем текущий вектор
Из канонического уравнения прямой L1 найдем координаты некоторой точки А, расположенной на L1: А(1 0 -2) и, соединив ее с текущей точкой М(x y z), образуем текущий вектор ![]() {x-1 y z+2}
{x-1 y z+2}![]() .
.
Из уравнений прямых получим направляющие вектора ![]() {3 2 -1},
{3 2 -1}, ![]() {1 –2 3}, которые, как и прямые L1, L2, принадлежат плоскости
{1 –2 3}, которые, как и прямые L1, L2, принадлежат плоскости ![]() . Так как для любой точки М(x y z)
. Так как для любой точки М(x y z) ![]() выполняется условие компланарности векторов (
выполняется условие компланарности векторов (![]() ,
,![]() ,
,![]() )=0, а
)=0, а ![]() не параллелен
не параллелен ![]() 2, то искомая плоскость описывается уравнением:
2, то искомая плоскость описывается уравнением:
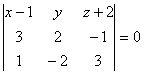
![]()
4) Найти уравнение плоскости α, проходящей через прямые
L1: ![]() и L2:
и L2: 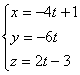 .
.
![]() На искомой плоскости возьмем текущую точку М(x y z) и соединим ее с некоторой точкой А(-1 1 0) прямой L1, координаты которой содержатся в каноническом уравнении этой прямой. Образуем текущий вектор
На искомой плоскости возьмем текущую точку М(x y z) и соединим ее с некоторой точкой А(-1 1 0) прямой L1, координаты которой содержатся в каноническом уравнении этой прямой. Образуем текущий вектор ![]() {x+1 y-1 z}
{x+1 y-1 z}![]() . Из уравнений прямых получим направляющие вектора
. Из уравнений прямых получим направляющие вектора ![]() { 2 3 -1},
{ 2 3 -1}, ![]() {-4 –6 2 }, которые принадлежат плоскости
{-4 –6 2 }, которые принадлежат плоскости ![]() . Заметим, что
. Заметим, что ![]() II
II![]() , значит в составлении уравнения искомой плоскости может участвовать только один из этих векторов, например,
, значит в составлении уравнения искомой плоскости может участвовать только один из этих векторов, например, ![]() . Отсюда возникает необходимость в том, чтобы найти еще один вектор, принадлежащий плоскости и не параллельный
. Отсюда возникает необходимость в том, чтобы найти еще один вектор, принадлежащий плоскости и не параллельный ![]() . Для этого на прямой L2 возьмем некоторую точку В. Координаты этой точки получим из уравнения прямой L2, имеем В(1 0 -3). Составим вектор
. Для этого на прямой L2 возьмем некоторую точку В. Координаты этой точки получим из уравнения прямой L2, имеем В(1 0 -3). Составим вектор![]() {2 –1 -3}
{2 –1 -3}![]() α.
α.
Для любой точки М(x y z) ![]() условие (
условие (![]() ,
,![]() ,
,![]() ) =0 дает уравнение искомой плоскости α:
) =0 дает уравнение искомой плоскости α:
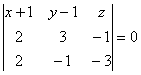
![]()
5) Найти уравнение плоскости α, проходящей через точку А(2 –1 0), перпендикулярно прямой L:
![]() .
.
![]() На искомой плоскости составим текущий вектор
На искомой плоскости составим текущий вектор ![]() {x-2 y+1 z}.
{x-2 y+1 z}.
Найдем направляющий вектор ![]() :
:
![]() =
=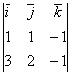 =
=![]() -2
-2![]() -
-![]() ,
, ![]() {1-2 -1}.
{1-2 -1}.
Для любой точки М(x y z) ![]() вектора
вектора ![]() и
и ![]() перпендикулярны, следовательно, для них выполняется условие
перпендикулярны, следовательно, для них выполняется условие ![]()
![]() =0, которое дает уравнение плоскости α.: (x-2)-2(y+1)-z=0.
=0, которое дает уравнение плоскости α.: (x-2)-2(y+1)-z=0. ![]()
6) Найти уравнение прямой L, проходящей через точку А(1 –3 2 ), перпендикулярно плоскости α :4x-y+2z+3=0.
![]() На прямой L образуем текущий вектор
На прямой L образуем текущий вектор ![]() {x-1 y+3 z-2}.
{x-1 y+3 z-2}.
Из общего уравнения плоскости α получим координаты ее вектора нормали ![]() {4 –1 2}.
{4 –1 2}.
Так как для любой точки М(x y z)![]() L вектора
L вектора ![]() II
II ![]() , то условие коллинеарности
, то условие коллинеарности
![]()
представляет собой уравнение искомой прямой. ![]()
7) Найти уравнение плоскости α, проходящей через прямую
L: ![]() перпендикулярно плоскости β: 2x-3y+z-1=0.
перпендикулярно плоскости β: 2x-3y+z-1=0.
![]() На плоскости α произвольным образом отметим точку М(x y z). Каноническое уравнение прямой L содержит координаты некоторой точки А(0 1 -2), лежащей на этой прямой. Соединив точки А и М, образуем текущий вектор
На плоскости α произвольным образом отметим точку М(x y z). Каноническое уравнение прямой L содержит координаты некоторой точки А(0 1 -2), лежащей на этой прямой. Соединив точки А и М, образуем текущий вектор ![]() {x y-1 z+2}.
{x y-1 z+2}.![]() .
.
Из уравнения прямой L найдем направляющий вектор ![]() {2 1 -3}. Так как L
{2 1 -3}. Так как L![]() , L II
, L II![]() , то
, то ![]()
![]() . Из общего уравнения плоскости β найдем координаты вектора нормали
. Из общего уравнения плоскости β найдем координаты вектора нормали ![]() {2 –3 1 }.Поскольку β
{2 –3 1 }.Поскольку β![]()
![]() , β
, β![]() α, то
α, то ![]()
![]() .
.
Для любой точки М(x y z) ![]() вектора
вектора ![]() ,
,![]() ,
,![]() компланарны. Так как
компланарны. Так как ![]() не параллелен
не параллелен ![]() , то условие (
, то условие (![]() ,
,![]() ,
,![]() )=0 порождает уравнение плоскости:
)=0 порождает уравнение плоскости:
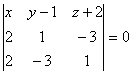
![]()
8) Дана прямая L2: 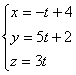 и плоскость α: x-4y+2z+3=0.
и плоскость α: x-4y+2z+3=0.
a) Проверить, являются ли L и α параллельными.
b) Проверить, являются ли L и α перпендикулярными.
c) Найти угол φ между L и α.
![]() a) Из заданных уравнений получим координаты направляющего вектора
a) Из заданных уравнений получим координаты направляющего вектора ![]() {-1 5 3} прямой L и вектора нормали
{-1 5 3} прямой L и вектора нормали ![]() {1 –4 2 } плоскости.
{1 –4 2 } плоскости.
Если![]()
![]()
![]() , то L IIα. В нашем случае условие перпендикулярности векторов не выполняется, так как
, то L IIα. В нашем случае условие перпендикулярности векторов не выполняется, так как ![]() ּ
ּ![]() =-15
=-15![]() 0. Стало быть, L не параллельна α.
0. Стало быть, L не параллельна α.
b) Если ![]() II
II![]() , то L
, то L![]() . В нашем случае условие параллельности векторов не выполняется, так как
. В нашем случае условие параллельности векторов не выполняется, так как
![]() . Следовательно, L не перпендикулярна α.
. Следовательно, L не перпендикулярна α.
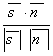
d) Угол между прямой и плоскостью вычислим по формуле:
sin![]() =sin(
=sin(![]()
![]() ,
,![]() )=
)= .
.
Отсюда sin![]() =
=![]() .
. ![]()
9) Найти точку пересечения прямой ![]() и плоскости 2x+3y+3z-9=0.
и плоскости 2x+3y+3z-9=0.
![]() Параметрическое уравнение прямой имеет вид:
Параметрическое уравнение прямой имеет вид:
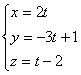 . Подставим эти значения X, Y, Z в уравнение плоскости:
. Подставим эти значения X, Y, Z в уравнение плоскости:
4t+3(-3t+1)+3(t-2)-9=0, получим t=-6. Откуда X=-12, Y=19, Z=-8. Следовательно, точка пересечения имеет координаты (-12 19 -8). ![]()