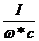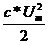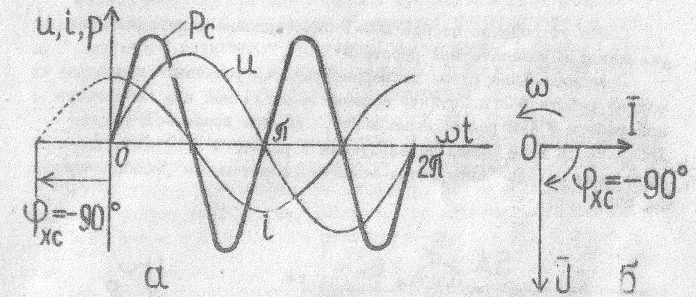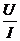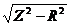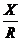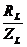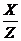I.I. Освоить метод «амперметра-вольтметра-ваттметра» для измерения электрических параметров электротехнических устройств.
I.2. Получить навыки расчета параметров электротехнических устройств по экспериментальным данным, составления их схем замещений и построения векторных диаграмм.
2. СОДЕРЖАНИЕ РАБОТЫ.
2.I. Методом «амперметра-вольтметра-ваттметра» произвести измерения тока, напряжения и активной мощности катушки индуктивности, конденсатора и лампы накаливания при включении их в электрическую сеть промышленности частоты.
2.2. По результатам измерений определить электрические параметры исследуемых электрических устройств: полные сопротивления, активные и реактивные сопротивления, индуктивность и емкость, углы сдвигов фаз и коэффициенты активной и реактивной мощности.
2.3. Составить схемы замещения исследованных устройств, построить их треугольники сопротивлений и векторные диаграммы.
3. ПРАВИЛА И МЕРЫ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ
Кроме выполнения общих правил и мер по технике безопасности при работе в электротехнических лабораториях, необходимо выполнять следующие правила:
3.I. Перед тем, как приступить к сборке схемы необходимо внимательно осмотреть панель стенда ЛЭС-I и убедиться, что ни в одну из 23 розеток коммутирующих разъемов XI…X2I не вставлена вилка (она ярко окрашена), так как это может привести к короткому замыканию в цепи при включении схемы.
3.2. Необходимо помнить, что при переходе от измерения параметров катушки индуктивности к конденсатору и далее к лампе накаливания надо выключить питание, затем вынуть вилку разъема XI6 и перенести ее в розетку разъема XI5, а при измерениях лампы накаливания – в розетку разъема XI4. Таким образом, в процессе выполнения данной лабораторной работы на панели будет находиться лишь одна коммутирующая вилка.
3.3. За нарушение правил и мер по технике безопасности студенты отстраняются от выполнения работы и на них налагается дисциплинарное взыскание.
4. ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
При подготовке к выполнению данной работы студент должен:
4.I. Изучить разделы курса электротехники, посвященные анализу цепей однофазного переменного тока (I,c.72-104;с.46-73;3,с.97-120), и при самоконтроле усвоения этого материала ответить на контрольные вопросы.
4.2. Изучить данные методические указания, четко усвоить при этом цель и содержание работы, последовательность ее выполнения, ознакомиться с описанием стенда ЛЭС-I, на котором будет выполняться работа, и продумать ожидаемые результаты предстоящих экспериментов.
4.3. Подготовить бланк отчета, в котором должны быть:
а) цель работы;
в) схема эксперимента (рис.7);
г) таблицы 2 и I, в которые записываются экспериментальные данные и результаты расчета.
4.4. Изучить правила и меры по технике безопасности, присущие данной работе, и строго их придерживаться.
4.5. В лаборатории ознакомиться со стендом ЛЭС-I и той его частью, на которой будет выполняться лабораторная работа.
4.6. При подготовке к выполнению работы необходимо обратить внимание на то, что переменным называется ток, периодически изменяющий свою величину и направление.
Широкому распространению переменного тока в энергетике способствовало то, что двигатели переменного тока самые простые, дешевые и надежные. Кроме того, переменное напряжение очень легко преобразовать из одной величины в другую, что имеет решающее значение при передаче электрической энергии.
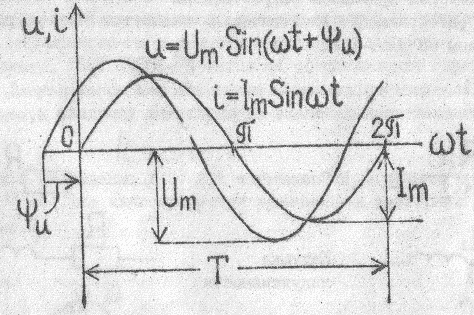
В энергетике применяется только синусоидальная форма тока, напряжения, э.д.с. (рис.I), которые описываются гармоническими функциями:
i=Im*sin ωt ; u=Um*sin(ωt+ψH)
Следует помнить, что мгновенным значением тока i называется значение тока в определенный момент времени (т.е. для рассматриваемого момента времени это величина постоянная).
Необходимо усвоить, что амплитудным значением, или амплитудой колебания тока, напряжения, э.д.с. называется их максимальные абсолютные значения за период. Обозначается Im, Um, Em.
Pис.1. Графики мгновенных значений синусоидального напряжения и тока
Фазой колебания называется аргумент синусоидальной функции ( на рис.1 фазы ωt и ωt +ψH) . Буквенного обозначения не имеет.
Начальная фаза (ψ) – фаза в момент времени t=0 (на графике ψH=ψu , ψi=0).
Сдвиг фаз двух синусоидальных функции есть разность их начальных фаз. Сдвиг фаз между напряжением и током по ГОСТу определяется и обозначается:
φ=ψu-ψi (1)
(на графике φ=ψu-ψi=ψu)
Период (T) – время полного цикла колебания.
Частота колебания (f [Гц]) – число циклов колебаний в секунду.
Угловая частота(ω) – частота колебаний, выраженная радианах:
ω =2πf[c-1] (2)
Промышленная частота f=50Гц, тогда угловая частота ω =314C-1.
О тепловом и электромеханическом действиях синусоидального тока судит по его среднему квадратичному значению, которое называют действующим, или эффективным значением:
I =
=0,707*Im (3)
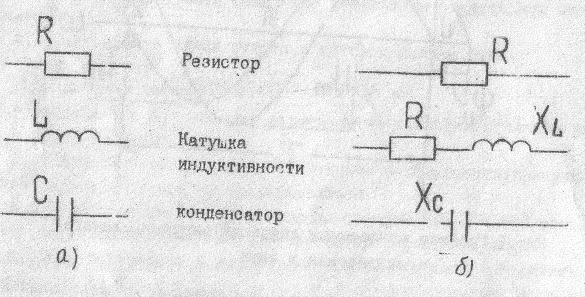
Наиболее распространенными электротехническими устройствами цепей переменного тока являются резисторы, катушки индуктивности и конденсаторы, условные графические и буквенные обозначения которых приведены на рис.2,а. Их схемы замещения, отображающие электрические параметры этих устройств, приведены на рис.2,б
Рис .2. Условие графические и буквенные обозначения электротехнических устройств (а) и их схемы замещения (б)
Активное сопротивление. Если резистор (резистор-устройство, служащее для использования его сопротивления.) переключить из цепи постоянного тока в цепь переменного, величина его сопротивления току изменится (увеличится из-за явлений поверхностного эффекта и эффекта близости) и тем более, чем выше частота тока. Поэтому электрический параметр резистора-сопротивление – в цепи постоянного тока называют омическим сопротивлением, а в цепи переменного - активным сопротивлением.
Согласно ГОСТ 19880-74 активное сопротивление определяется из закона Джоуля-Ленца как отношение мощности, поглощаемой этим сопротивлением, к квадрату действующего значения протекающего в нем тока, т.е.
R=
(4)
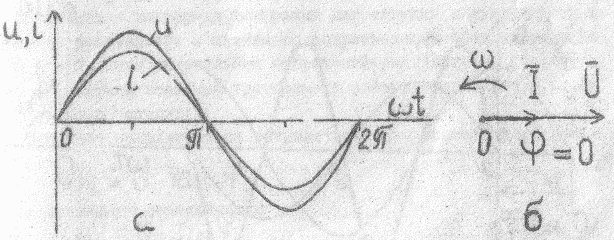
Ток и напряжение в цепи с активным сопротивлением совпадает по фазе (φ=0), что иллюстрируется временной и векторной диаграммами (ВД) рис.3
Рис .3. Графики мгновенных значений напряжения и тока (а) и векторная диаграмма (б) цепи с активным сопротивлением
Индуктивное сопротивление. Если по катушке индуктивности пропустить синусоидальный ток, то он наведет в катушке э.д.с. самоиндукции
eL= -L
(5)
которая направлена встречно (из закона Ленца) возникающему току.
Отсюда эффект влияния э.д.с. самоиндукции подобен действию сопротивления - уменьшает ток в цепи.
Величина э.д.с. самоиндукции из формулы (5) равна:
EL=I*ωL
и ее принято учитывать как падение напряжения UXL на воображаемом (вымышленном) сопротивлении, которое называют индуктивным:
XL= ω L [Ом] (6)
тогда
EL=UXL=I*XL (7)
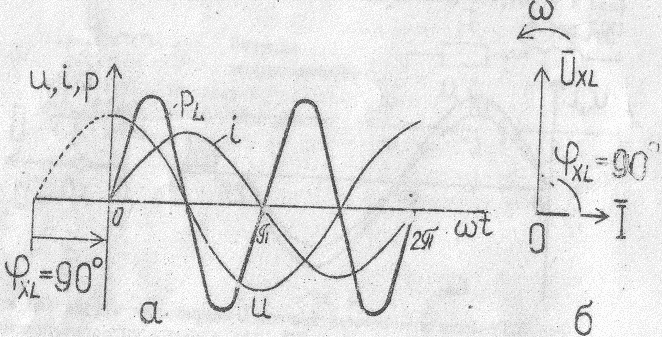
Из закона Фарадея (5) легко показать, что индуктивное напряжение (7) опережает по фазе ток на 900 (см. рис.4)
Рис .4. График мгновенных значений индуктивного напряжения, тока и мощности (а) и векторная диаграмма (б)
Если напряжение (7) умножить на ток, получим индуктивную мощность
QL=PL=I*UXL=I2*XL[BAp] (8)
Временной график ее представлен на рис.4. Как видно, четверть периода эта мощность положительна, поступает от генератора. Катушка в это время накапливает энергию в магнитном поле, достигая максимума вместе с током:
WLmax=
(2)
и с этого момента мощность становится отрицательной, так как магнитное поле начинает уменьшаться, и катушка всю запасенную в ней энергию (9) возвращает назад генератору (дважды за период).
В связи с непрерывным обменом энергией между катушкой и генератором эту энергию, мощность и индуктивное сопротивление называют реактивными.
Реактивная мощность является паразитной, так как не создает полезной (активной) работы, кроме того, индуктивный ток загружает сечение проводов ЛЭП и генератора и увеличивает потери в них.
Так как провода обмотки катушки обладают активным сопротивлением, то полное сопротивление катушки индуктивности будет
Z=
(10)
Оно же в комплексной форме (алгебраической и показательной)
=R+јXL=Z*eјφL (11)
Закон Ома для катушки индуктивности
U=I*Z (12)
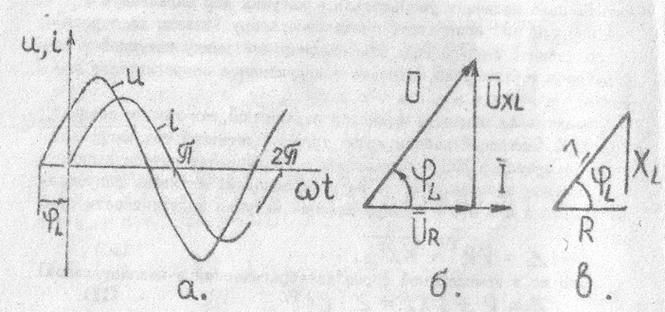
Временная и векторная диаграммы для катушки индуктивности с учетом ее реактивного и активного сопротивлений представлены на рис. 5, а и б. Если треугольник напряжений разделить на ток, то, очевидно, получим подобный треугольник сопротивлений (рис. 5, в). Из треугольников находят:
- активное напряжение на катушке (активную составляющую напряжения)
UR=U*cosφ (13)
- индуктивную составляющую
UXL=U*sinφ (14)
- коэффициенты активной и реактивной мощности:
cosφL=
(15)
sinφL=
(16)
- сдвиг фаз на катушке
φL=arctg
(17)
Емкостное сопротивление. Если через конденсатор протекает синусоидальный ток, то на обкладках конденсатора появляется напряжение заряда
UC=
(18)
которое направлено встречно приложенному напряжению. Отсюда, эффект влияния подобен действию сопротивления – уменьшает ток в цепи.
Рис.5. График мгновенных значений тока и напряжения катушки индуктивности (а), ее векторная диаграмма (б) и треугольник сопротивлений (в)
Величина напряжения заряда из уравнения (18) равна
Uc=
и его принято учитывать, как падение напряжение UXC, на воображаемом сопротивлении, называемом емкостным
XC=
[Ом] (19)
тогда
Uc=UXC=I*Xc (20)
Из уравнения (18) легко показать, что емкостное напряжение (20) отстает по фазе от тока на 900 (см. рис.6).
Если емкостное напряжение (20) умножить на ток, то получим емкостную мощность:
Qc=I*UXC=I2*XC[BAp] (21)
Из временного графика емкостной мощности (см. рис.6) видно, что конденсатор подобно катушке индуктивности запасает энергию (при заряде) в электрическом поле
WCmax=
затем возвращает ее генератору, в силу чего эта энергия, мощность и емкостное сопротивление называются реактивными.
Рис.6. График мгновенных значений емкостного напряжения, тока и мощности (а) и векторная диаграмма (б)
Так как на промышленной частоте потерь в конденсаторе нет (диэлектрик не нагревается) PC=I2R=0, следовательно, активным сопротивлением он не обладает( R=0).
Полное сопротивление конденсатора равно емкостному
Z=XC
или в комплексной форме
=-јXC=XC e-ј90˚ (22)
Очевидно, так как у конденсатора активного сопротивления нет (R=0), его треугольники напряжений и сопротивлений вырождаются в прямые:
=
XC и Z=XC.
5. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
5.1 Лабораторный электротехнический стенд ЛЭС – I
Общее устройство стенда ЛЭС – I было описано в методических указаниях к лабораторной работе № I.
Принципиальная схема экспериментальной установки к лабораторной работе № 3 на стенде совмещена со схемой для лабораторной работы №4 и расположена внизу, в центре приборной панели ЛЭС – I. Часть этой схемы, используемая в работе № 3, представляющая схему метода «амперметра – вольтметра – ваттметра», изображена на рис.7.
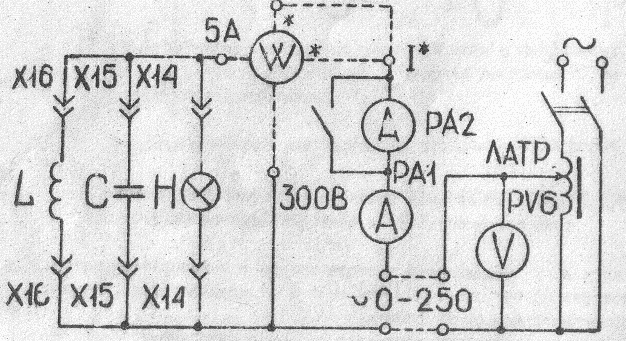
Рис.7 принципиальная схема ЛЭС – I измерения параметров электрических устройств методом амперметра – вольтметра – ваттметра
Здесь питающее напряжение сети подается через лабораторный автотрансформатор – ЛАТР, который позволяет регулировать его величину в пределах от 0 до 250 В, а его значение контролируется с помощью вольтметра PV6. Измерение тока цепи осуществляется приборами РА2 (величиной до IA) или PAI в зависимости от величины тока (если прибор РА2 «зашкаливает», его замыкают выключателем S1).
Активную мощность, потребляемую включенным электрическим устройством, параметры которого измеряются, показывает ваттметр W, который на стенде ЛЭС – 1 не установлен и должен быть подключен своими зажимами «I», «ЗОО В» и «5А» и соответствующим зажимам ЛЭС – 1.
Исследуемые устройства – катушка индуктивности L, электрический конденсатор С или помпа накапливания Н – включаются в схему «амперметра – вольтметра – ваттметра» поочередно. С помощью вилки разъема, вставляемой соответственно в розетки разъемов Х16 (для включ. L) Х15 или Х14 (для включения Н).
Как следует из принципиальной электрической схемы измерения (см. рис.7) для ее сборки достаточно тремя соединительными проводами подключить к ЛЭС – 1 ваттметр W и двумя – подать на зажимы «~250» переменное напряжение от ЛАТРа. Таким образом, сборке подлежит только часть схемы, изображенная пунктирными линиями..
5.2 Метод амперметра – вольтметра – ваттметра
Для определения параметров электротехнических устройств широко пользуется метод амперметра – вольтметра – ваттметра.
Схема измерения по этому методу показана на рис. 8.
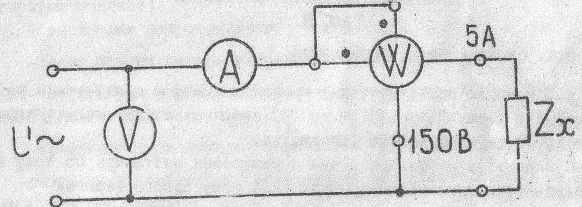
Рис.8.Схема изменения по методу ампера-вольтметра-ваттметра.
К выходным зажимам этой схемы подсоединяется измеряемое электротехническое устройство. Зачем, одновременно снимают показания вольтметра UV, амперметра IA и ваттметра PW.
Ваттметр представляет собой четырехзажимный прибор электродинамической системы, которая содержит две катушки, магнитные поля которых, взаимодействуя, создают крутящий момент. Одна катушка включается в цепь последовательно (токовая), а другая – параллельно (катушка напряжения). Зажимы, отмеченные точкой или звездочкой являются началами обмоток и обязательно должны включаться в сторону генератора (источника питания), чтобы было правильное отклонение стрелки (вправо).
Ваттметры лабораторных классов точности обычно не градуируются, и чтобы определить мощность, находят цену делений ваттметра по формуле
C=
[Вт/дел], (23)
где IHOM– номинальный ток выбранного предела измерения;
UHOM – номинальное напряжение выбранного предела измерения;
αHOM – полное число делений шкалы приборов.
Тогда мощностьPί=C αL
После производства измерений рассчитывают:
- полное сопротивление из закона Ома (12);
- активное сопротивление из закона Джоуля - Ленца (4);
- реактивное сопротивление из треугольника сопротивлений по формуле Пифагора (10);
- индуктивность катушки по формуле (6);
- емкость конденсатора по формуле (19).
6. ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ
6.1.Проведение экспериментов
а) С помощью соединительных проводов (5шт.) и одной вилки разъема собрать схему “V-A-W”, включив катушку индуктивности в качестве измеряемого устройства.
б) Используя выбранные пределы измерения ваттметра по току и напряжению, определить по формуле (23) цену одного деления прибора в ваттах.
в) Включить напряжение питания, установить заданное преподавателем напряжение и произвести измерения тока, напряжения и мощности.
г) Включить в схему конденсатор, переставив вилку разъема из розетки X16 в Х15, подать напряжение и провести измерения.
Выключить питание схемы.
д) Вместо конденсатора включить пампы накаливания (число задается преподавателем), и произвести измерения. Выключить питание.
Результаты экспериментов занести в таблицу 1.
Таблица 1
| Элемент |
Измерено |
Рассчитано |
||||||||
| U, В |
I, А |
P, Вт |
Z |
R |
X |
cosφ |
sinφ |
UR |
UX |
|
| L |
||||||||||
| C |
||||||||||
| H |
||||||||||
6.2. Обработка результатов
а) По результатам измерений рассчитать:
- полное сопротивление устройств Z=
- активные сопротивления R=
ПРИМЕЧАНИЕ: при определении полного и активного сопротивлений лампы накаливания в силу различия точности измерений приборов эти сопротивления, как правило, не равна(ZH≠RH). Поэтому за истинное значение этих сопротивлений следует принять их среднеарифметическое
- реактивные сопротивления X=
- сдвиг фаз на каждом устройстве φ=arctg
- коэффициент мощности катушки и других устройств с индуктивным сопротивлением cosφL=
- коэффициент реактивной мощности sinφ=
- активные и реактивные составляющие напряжения, действующие в устройствах:
UR=U*cosφ
UX=U*sinφ
- индуктивность катушки L=
=
[Гн]
- емкость конденсатора C=
=
[мкФ]
Результаты этих расчетов занести в табл. 1 и 2.
б) Используя результаты измерений и расчетов, сведенные в табл. 1, заполнить табл.2.
При заполнении граф табл.2, связанных с построением векторных диаграмм и треугольников сопротивлений, соблюдать масштаб.
Таблица 2
| Электротехническое устройство |
|||
| Катушка индуктивности |
Конденсатор |
Лампа накала |
|
| Условное обозначение (граф. и букв.) |
|||
| Индуктивность и емкость устройства |
|
|
|
| Полное сопротивление Z |
|||
| Активное сопротивление R |
|||
| Реактивное сопротивление X |
|||
| Схема замещения |
|||
| Треугольник сопротивлений М: 1см=…Ом |
|||
| Комплексное сопр. (алгебраич. форма) |
|
||
| Комплексное сопр. (показ. форма) |
|
||
| Сдвиг фаз |
φL= |
φC= |
φH= |
| Векторные диаграммы М: 1см=…В 1см=…А |
|||
6.3. ВЫВОДЫ ПО РАБОТЕ
Анализируя полученные экспериментальные данные об электрофизических параметрах исследованных электрических устройств, следует осветить следующие вопросы:
6.3.1. Дать физическое объяснение отставания по фазе тока от индуктивного напряжения в катушке.
6.3.2. Дать физическое объяснение отставания по фазе емкостного напряжения от тока в конденсаторе.
6.3.3. Дать физическое объяснение совпадения по фазе тока и напряжения в цепи с активным сопротивлением.
6.3.4. Какие энергетические процессы протекают в электротехнических устройствах, содержащих реактивные элементы?
6.3.5. Какие энергетические процессы протекают в электротехнических устройствах, обладающих активными сопротивлениями?
6.3.6. В чем физическая сущность индуктивного сопротивления?
6.3.7. Объясните физическую сущность емкостного сопротивления.
6.4.Содержание отчета
а) Цель работы;
б) Схема эксперимента (рис.1)
в) Таблицы №1 и №2 с результатами экспериментов и их обработки;
г) Выводы по работе в виде ответов на вопросы п.6.3.
7.КОНТРОЛЬНЫЕ ВОПРОСЫ
7.1. Что такое мгновенное значение тока (напряжения, э.д.с.)?
7.2. Что такое амплитуда тока?
7.3. Что называется фазой?
7.4. Что называется начальной фазой?
7.5. Что называется сдвигом фаз?
7.6. В чем различия между принципиальной электрической схемой и ее схемой замещения?
7.7. Что такое эффективное (действующее) значение тока (напряжения)?
7.8. Что такое реактивная мощность?
7.9. Что такое активная мощность?
7.10. Как сдвинуты по фазе ток и напряжение в индуктивном сопротивлении (емкостном, активном)?
7.11. Каким методом измеряют параметры электротехнических устройств в цепях промышленной частоты?
7.12. Напишите формулы расчета всех параметров электротехнического устройства по результатам эксперимента.
7.13. Как определить через емкость и индуктивность их реактивные сопротивления?
7.14. Что такое треугольник сопротивлений, как его можно получить и как строить?
7.15. Как определить цену деления ваттметра?