Лабораторная работа по САУ №3
«Идентификация многомерных объектов»
Цель работы.Получить модель двумерного объекта методом планирования эксперимента.
Краткая теория.Для описания участка поверхности отклика многомерного объекта со значительной кривизной используются полиномы второго порядка вида:
Y(x1,x2)=b0+b1x1+b2x2+b12x1x2+b11x12b22x22 (1)
При проведении эксперимента входные воздействия должны быть независимы. В процессе эксперимента каждому входному воздействию xi задаются различные уровни (значения).
Если во время эксперимента перебираются все возможные неповторяющиеся сочетания уровней для п независимых управляющих воздействий (факторов), то он называется полным факторным экспериментом (ПФЭ).
При одинаковом числе уровней - D, число точек спектра плана ПФЭ равно
Для определения значений коэффициентов можно воспользоваться методом минимума суммы квадратов. Более просто получить результат, если считать, что минимум отклонений имеет место при совпадении результатов расчётной модели и эксперимента в точках проведения опытов. В этом случае коэффициенты bi должны удовлетворять системе уравнений вида:
где Y – матрица-столбец экспериментальных значений с числом элементов N, равным числу опытов;
В – матрица – столбец коэффициентов bi с числом элементов равным числу членов полинома m (для полинома второго порядка m = (n+1)*(n+2)/2);
X – матрица входных воздействий размером N x m.
Матрицу В можно найти по формуле:
Если подобрать значения xi таким образом, что матрица С будет диагональной, то система (4) разобьётся на m независимых уравнений, каждое из которых будет включать лишь один неизвестный коэффициент bi
Для того, чтобы матрицу С сделать диагональной переходят к относительным величинам входных переменных:
|
.jpg)
|
(5) |
Где .jpg) a xi2 заменяются т.н. центрированными квадратичными функциями. Тогда матрица Х будет иметь вид:
a xi2 заменяются т.н. центрированными квадратичными функциями. Тогда матрица Х будет иметь вид:
| x0 |
x1 |
x2 |
... |
xn |
x1x2 |
... |
xn-1xn |
x12 |
x22 |
... |
xn2 |
| 1 |
-1 |
-1 |
... |
-1 |
1 |
... |
1 |
1 |
1 |
... |
1 |
| 1 |
1 |
-1 |
... |
-1 |
-1 |
... |
1 |
1 |
1 |
... |
1 |
| 1 |
-1 |
1 |
... |
-1 |
-1 |
... |
1 |
1 |
1 |
... |
1 |
| 1 |
1 |
1 |
... |
-1 |
1 |
... |
1 |
1 |
1 |
... |
1 |
| ... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
| 1 |
1 |
1 |
... |
1 |
1 |
... |
1 |
a2 |
 |
... |
 |
| 1 |
-a |
0 |
... |
0 |
0 |
... |
0 |
a2 |
 |
... |
 |
| 1 |
a |
0 |
... |
0 |
0 |
... |
0 |
 |
a2 |
... |
 |
| 1 |
0 |
-a |
... |
0 |
0 |
... |
0 |
 |
a2 |
... |
 |
| 1 |
0 |
a |
... |
0 |
0 |
... |
0 |
 |
 |
... |
a2 |
| ... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
| 1 |
0 |
0 |
... |
a |
0 |
... |
0 |
 |
 |
... |
 |
| 1 |
0 |
0 |
... |
0 |
0 |
... |
0 |
 |
 |
... |
 |
Тогда коэффициенты определяются по формулам:
.jpg) (6)
Для полинома 2-й степени, описывающего двумерный объект: а=1;
(6)
Для полинома 2-й степени, описывающего двумерный объект: а=1; 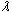 =0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
Задание.Получить математическую модель поверхности отклика
=0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
Задание.Получить математическую модель поверхности отклика
.jpg)
.jpg)
.jpg)

































.jpg) (6)
(6) 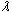 =0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
=0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
.jpg)
.jpg)

































.jpg) (6)
(6) 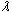 =0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
=0,66667; k0=0,11111; k1=0,16667; k2=0,25; k3=0,5
.jpg)