Меню

Введение

Цель преподавания дисциплины

Дать основные понятия и закономерности инженерной механики сплошной среды, в особенности, твердых тел, с целью применения полученных знаний для решения практических задач различных технологических процессов машиностроения.

Задачи изучения дисциплины

В результате изучения дисциплины студенты должны:

Основные понятия и определения

Понятия материальной точки, абсолютно твердого тела, сплошной среды. Гипотеза сплошности, однородность сплошной среды. Тела изотропные и анизотропные. Силы внешние и внутренние. Понятие напряжений и деформаций.

Теория напряженного состояния

Компоненты напряжений на гранях элементарного параллелепипеда Закон парности касательных напряжений. Тензор напряжений, шаровой тензор, девиатор напряжений, и их физический смысл.

Напряжения в наклонных площадках. Главные нормальные напряжения. Инвариантные характеристики напряженного состояния. Эллипсоид напряжений. Главные касательные напряжения. Октаэдрические напряжения. Интенсивность напряжений.

Дифференциальные уравнения движения и равновесия твердых тел. Примеры использования тензорных характеристик для решения практических задач.

Кинематика сплошной среды

Точки зрения Эйлера и Лагранжа на движение сплошной среды. Траектории движения материальных частиц, линии тока. Стационарные и нестационарные процессы. Трубки тока.

Понятия перемещения точек однородных деформаций. Конечные деформации сплошной среды. Малые деформации. Логарифмические деформаций. Условие несжимаемости пластически деформируемых тел. Дифференциальные уравнения неразрывности малых деформаций. Тензорные характеристики деформированного состояния. Инварианты. Интенсивность деформаций. Вихрь поля скоростей.

Связь между напряжениями и деформациями

Определяющие уравнения в механике сплошной среды. Линейно-упругие и нелинейно-упругие материалы. Модели идеальных тел. Сложные реологические модели сплошной среды. Механические аналоги реологических моделей.

Понятия ползучести, последействия, релаксации. Влияние эффектов последействия и релаксации на поведение металлов и композитных материалов.

Эффект Боушингера и петля упругого гистерезиса. Реологические свойства и зависимости для реальных материалов. Гипотеза единой кривой.

Физические уравнения по теории малых упругопластических деформаций. Физические уравнения по теории пластического течения.

Теория предельных напряженных состояний

Виды предельных напряженных состояний. Факторы, влияющие на виды напряженного состояния материала. Понятие об эквивалентном напряжении.

Условие пластичности наибольших касательных напряжений - условие Треска-Сен-Венана-Леви.

Энергетическое условие пластичности - условие Губера-Мизеса-Генки.

Физический и геометрический смысл условия пластичности.

Влияние схемы напряженного состояния на пластичность и технологическую деформируемость.

Элементы теории разрушения О.Мора, ее применение для оценки вероятности разрушения материалов, которые деформируются в различных условиях.

Краевые задачи

Понятие краевой задачи. Аналитические, приближенные и численные методы решения краевых задач.

Проблемы машиностроительного производства как исходные данные для постановки краевых задач: Физическая сущность краевой задачи.

Система исходных уравнений пластически деформируемых тел. Граничные условия в технологических задачах обработки давлением. Действительные статистически допустимые и кинематически возможные решения практических задач.

Численные методы решения краевых задач. Метод конечных элементов, метод конечных разностей, метод граничных элементов.

Контрольная работа по курсу «Инженерная механика твердого тела»

Вариант №1
  1. Компоненты напряжений в цилиндрической системе координат. Закон парности касательных напряжений.
  2. Малые деформации (вывод формул).
  3. Построить диаграмму Мора для элементарной площадки, находящейся под действием полного напряжения величиной 300 МПа и касательного напряжения равного 120 МПа. Углы наклона площадки относительно главных осей равны 30° и 60°
Вариант №2
  1. Линейно-упругие и нелинейно-упругие материалы. Модели идеальных тел. Механические аналоги реологических моделей.
  2. Главные нормальные напряжения. Инвариантные характеристики напряженного состояния (вывод формул).
  3. Прямоугольная заготовка с начальными размерами В = 200мм, L > 250мм, Н = 10мм получила деформацию определенную тензором Tε. Найти ее конечные размеры, если:

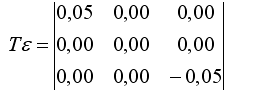
Вариант №3
  1. Тензор напряжений, шаровой тензор, девиатор напряжений. Инварианты тензора напряжений, девиатора напряжений.
  2. Точки зрения Эйлера и Лагранжа на движение сплошной среды. Траектории материальной частицы, линии тока, трубки тока.
  3. В некоторой точке деформируемого тела поле скоростей перемещений частиц описывается формулами:

    Записать тензор скоростей перемещений (vij).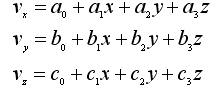
Вариант №4
  1. Понятия ползучести, последействия, релаксации.
  2. Глааные касательные напряжения (вывод формул). Площадки действия главных касательных напряжений.
  3. В точке тела заданы компоненты деформации εx εy εxy, а остальные компоненты равны нулю. Записать инварианты тензора деформаций и вывести формулы для главных деформаций.
Вариант №5
  1. Дифференциальные уравнения движения и равновесия.
  2. Интенсивность касательных напряжений. Интенсивность деформаций.
  3. Деформация прямоугольной заготовки с размерами В = 100мм, L = 150мм, Н = 40мм описывается тензором:

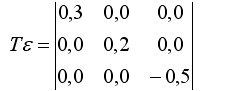
Вариант №6
  1. Эффект Боушингера и петля упругого гистерезиса.
  2. Энергетическое условие пластичности - условие Губера-Мизеса-Генки.
  3. Построить эллипсоид Ляме, если σ1 = З00МПа, σ2 = 400МПа, σ3 = 800МПа. Графически определить ориентацию площадки, если S1 = 200МПа, S2 = 400МПа.
Вариант №7
  1. Элементы теории разрушения O.Mopa, ее применение для оценки вероятности разрушения материалов, деформируемых в различных условиях.
  2. Скорость деформаций, их физический смысл. Тензорные характеристики скоростей деформации.
  3. Задано напряженное состояние точки:

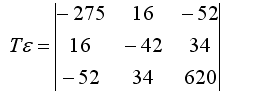
Вариант №8
  1. Материальная точка, абсолютно твердое тело, сплошная среда. Гипотеза сплошности однородность сплошной среды. Тела изотропные и анизотропные.
  2. Напряжения в наклонных площадках (вывод формулы).
  3. Тензор скоростей деформаций в некоторой точке и некотором базисе имеет матрицу компонент:

    Определить, чему равны I1, I2, I3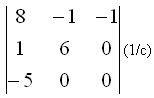
Вариант №9
  1. Понятие краевой задачи. Аналитические, приближенные и численные методы решения краевых задач.
  2. Логарифмические деформации. Условие несжимаемости пластически деформируемых тел.
  3. Определить, находится ли точка в пластическом состоянии, если ее напряженное состояние описывается тензором Тσ, если предел текучести материала σT = 250МПа.

Вариант №10
  1. Дифференциальные уравнения неразрывности малых деформаций (вывод формул).
  2. Влияние схемы напряженного состояния на пластичность и технологическую деформируемость.
  3. Напряженное состояние в точке тела определено тензором напряжений:

    Определить течение полного нормального и касательного напряжений на площадке с внешней нормалью «N», направляющие косинусы которой имеют одинаковое значение.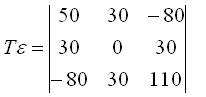

Учебно-методические материалы

Основная литература:

Дополнительная литература