Меню

• Краткие теоретические сведения
• Ррасчетши алгоритм
• Цель работы
• Методика выполнения работы
• Примеры расчетов
• Список рекомендуемой литературы

Тема: «Расчет процессов пластической деформации методом граничных элементов»

Краткие теоретические сведения

Задача расчета кинематических и силовых параметров процессов об­работки металлов давлением является физически нелинейной и может быть записана в виде суммы линейного L(u) и N(u) нелинейного опера­торов:

где Р — известная функция. Задаваясь начальным значением u ( в частности, u = 0), получим:

Решение повторяется до достижения требуемой точности величины u.

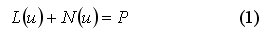
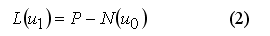
Рассмотренный подход соответствует методу упругих решений А. А. Ильюшина, при котором неупругая задача сводится к последова­тельности упругих. Технологические задачи о больших деформациях при высокой температуре должны рассматриваться как задачи о течении не­линейно-вязкой жидкости. Поэтому разрешающие уравнения для задач об­работки металлов давлением записываются аналогично тому, как это принято в гидродинамике:

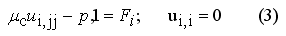
В качестве характеристики вязкости деформируемого металла ис­пользован известный в теории обработки металлов давлением коэффи­циент жесткости:

где σ_i — интенсивность напряжений, ε_i — интенсивность скоростей де­формаций.

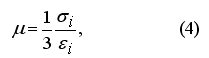
Для решения упругой задачи, соответствующей рассматриваемой, при­меняется гранично—элементное уравнение:

где p_i — напряжения, U_i — перемещения.

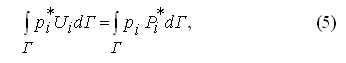
В настоящем решении используется известная аналогия между тече­нием вязкой жидкости и упруго-деформируемым несжимаемым телом (коэф­фициент Пуассона равен 0,5). Благодаря такому подходу величины U_i равны скоростям пластического течения в искомых точках на границе области. Для практического решения интегралы уравнения (5) заме­няются суммами:

где: N — количество граничных элементов, ΔSⁱ — площадь j-го отрезка длина которого составляет 2а. σ^j_s,σ^j_n, U^j_s,U^j_n - значения напряжений и смещений в центре j-го отрезка.

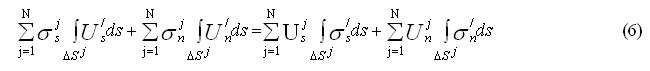
Входящие в уравнения (5) и (6) величины со звездочками полагают­ся искомыми, определяющиеся решением Кельвина. Для решения линейных задач используются только зависимости (5) и (6). В данном же случае, для решения нелинейной задачи пластической деформации используется итерационный цикл, подчиняющейся зависимости:

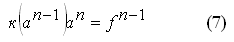
Один из способов реализации метода упругих решений, расчет на ос­нове алгоритма с дополнительными массовыми силами и поправками к граничным условиям. В этом случае соответствующие зависимости имеют вид:

где u(1)_n — величина поправки, рассчитываемая по компонентам массовым сил. Из уравнений (7) и (8) видно, что расчет задач пластического течения методом граничных элементов отличается от расчета этим же способом упругих задач.

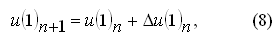
Отличие связано с тем, что в задачах плас­тического течения необходимо рассчитывать параметры не только на границе расчетной области но и внутри ее. Компоненты массовой силы в каждой внутренней ячейки области определяются как:

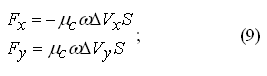
где . Для первого расчетного шага ΔV_x и ΔV_x — оператор Лапласса для соответствующих компонентов ско­ростей во внутренних ячейках с площадью S.

В работе расчеты выполнены с использованием линеаризующих алго­ритмов с дополнительными массовыми силами и переменной вязкости. В этом случае на каждом последующем шаге вновь решается задача для того же упругого тела, но уже находящегося под действием новой наг­рузки:

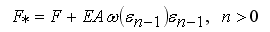
Расчетши алгоритм

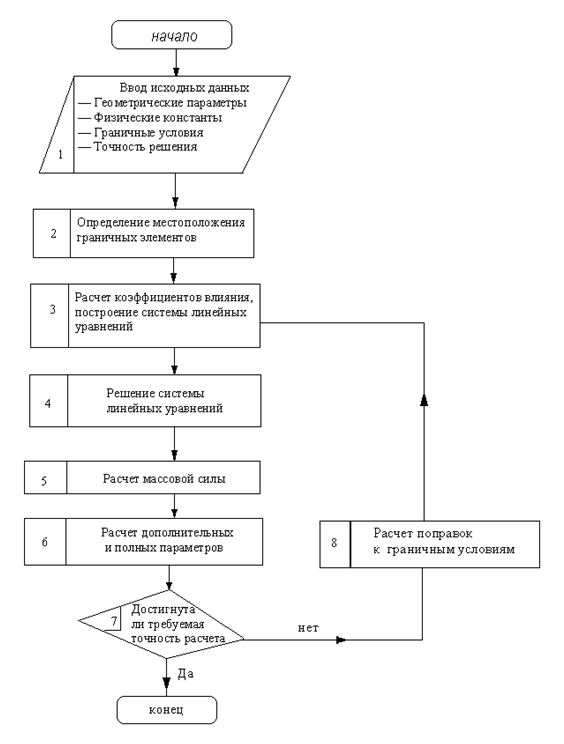
Укрупненный алгоритм решения задачи показан на рис. 1.

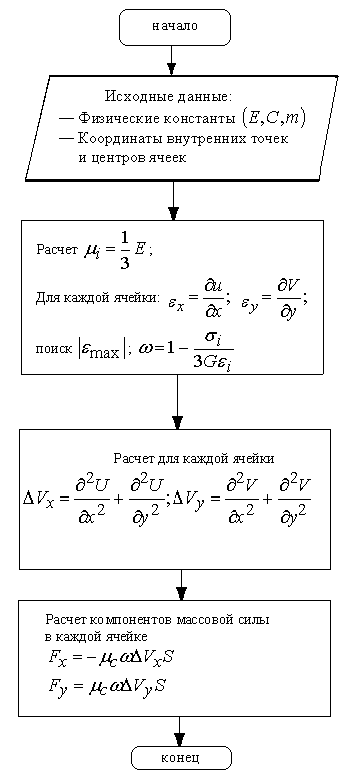
Расчет компонентов массовой силы производим в последовательности соответствующей блок-схеме показанной на рис.2

Последовательность вычислений по алгоритму переменной вязкости можно геометрически проиллюстрировать рис.3.

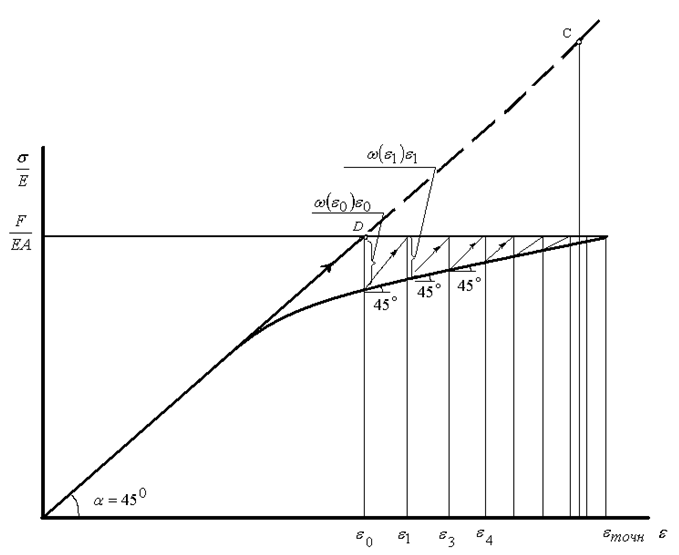
Рис. 3

Действительно, для каждого значения деформации находится значе­ние отрезка CB = ω(ε_n)ε_n и в следующем приближении полагается, что

или

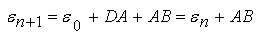
Как видно из рис. 3, процесс последовательных приближений (итерационный процесс) сходится к точному значению деформации ε_точн, если функция ω(ε) непрерывна и удовлетворяет условиям:

где λ ≤ 1 — константа.

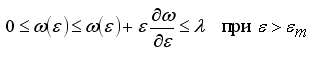
Однако можно заметить, что скорость сходимости существенно зави­сит от вида функции ω(ε). Если материал обладает большим упрочне­нием, т. е кривая мало отклоняется от прямой σ = Eε или, что то же са­мое, функция ω(ε) мала, то уже третье, четвертое приближение дает достаточно точное значение деформации.

И наоборот, если материал обладает малым упрочнением, то может потребоваться значительное число итераций (приближений), чтобы получить значение деформаций с требуемой точностью / 4 /.

Следует отметить. что рассмотренная методика является универ­сальной и пригодна для расчета поковок любой конфигурации.

Цель работы

Изучить методику расчетов процесса пластической деформации с при­менением метода граничных элементов и рассчитать перемещения при штамповке заданной поковки.

Методика выполнения работы

1. Разбить границу расчетной области на заданное количество граничных элементов.
2. Разбить расчетную область на определенное количество ячеек.
3. Заполнить файл исходных данных.

   

4. Выполнить расчеты на ПЭВМ по имеющейся программе.
5. Сравнить результаты расчетов с тестовыми или экспериментальны­ми данными.

Примеры расчетов

1

В качестве первого тестового примера используем задачу стяжении плоского кольца внутренним усилием рис.4

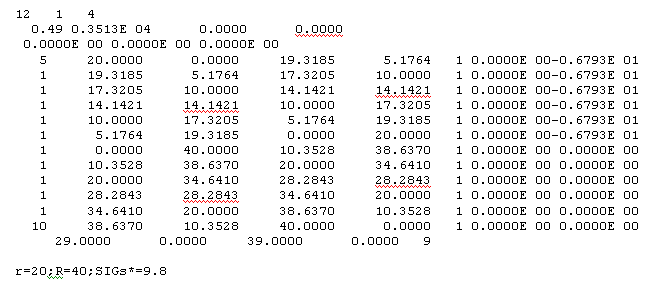
Размеры кольца: r = 20 мм и R = 40 мм, со следующими граничными условиями — нормальное напряжение на внутреннем контуре:

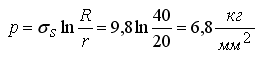
Касательные напряжения на поверхности контакта отсутствуют. На наружном контуре σ_n = σ_s = 0. Вследствие симметрии достаточно рассмот­реть только четверть кольца. Граничные элементы, аппроксимируются четвертью кольца показанного на рис.4. а данные по ним приведены в табл. 1.

Таблица 1.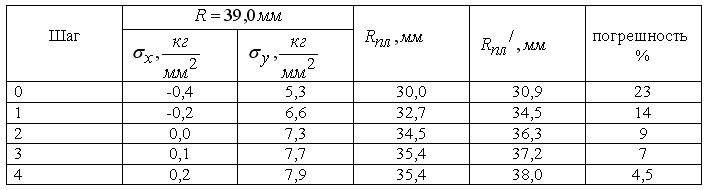

Как видно из граничным условий, эта задача в напряжениях. Кроме того, была выбрана одна линия полевых точек, находящаяся на оси сим­метрии х. В двадцати точках, лежащих на этой линии, были вычислимы смещения и напряжения, по которым, в свою очередь, была найдена массовая сила и поправки.

Полученные результаты хорошо согласуются с теоретическим расче­тов выполненные методом линий скольжения / 2 /.

2. Задача о полосе

Во втором тестовом примере (рис. 4.1) наружный контур был описан 50 граничными элементами, а внутренняя область была разбита на 20 ячеек в которых вычислялись смещения, напряжения и массовые силы.

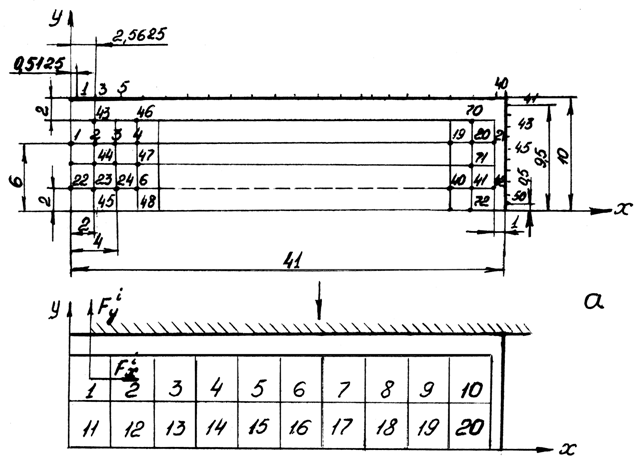
Рис 4.1

Трение на контакте было максимальным. Нормальные и касательные напряжения на свободной поверхности отсутствуют. Были наложены ус­ловия симметрии, что позволило упростить ввод данных и рассмотреть четверть заготовки. На третьем шаге расчетов была достигнута тре­буемая точность и сходимость итерационного цикла. Определяющим па­раметром было образование «бочки» на боковой поверхности (по 2мм) на сторону (рис. 4.2). Полученные результаты хорошо согласуются с ре­зультатами экспериментов Унксова /3/.

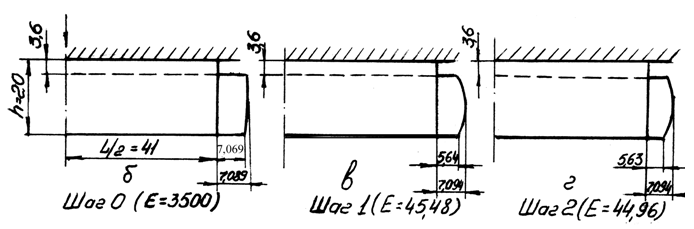
Рис 4.2

Фрагмент файла исходных данных для расчета задачи о полосе представлены ниже.

Сделать выводы по работе.

Список рекомендуемой литературы

1. Крауч С., Старфилд А. Методы граничных элементов в механике твердого тела. М.: Мир. 1987. 328 с.
2. Сторожев М. В., Попов Е. А. Теория обработки металлов давлением. Учебник для вузов. Изд. 4—е, перераб. и доп. М.: Машиностроение 1977.—423 с.
3. Унксов Е. П. Инженерная теория пластичности. М.:Машгиз.1959. 328 с.
4. Александров А.В., Потапов В. Д. Основы теории упругости и пластичности. М.: Высшая школа. 1990. 400 с.
5. Безухов Н. И. Основы теории упругости и пластичности. Изд. "Выс­шая школа" 1968.