|
3.1.3. Параметры динамических нагрузок и напряжений Эксплуатационные нагрузки машин и напряжения в деталях носят переменный и, как правило, случайный характер. Кроме точки приложения, направления и средней величины напряжение должно быть описано характером изменения во времени между минимальным и максимальным значениями. Согласно теории вероятностей случайная величина X за время t принимает множество значений Xi. Так как время t конечно, то и число значений Xi конечно и составляет N (целое положительное число). Статистическими характеристиками массива значений Xi , разбитого на k равных интервалов (разрядов) размером ΔX будут: - разрядная частость попадания значений Xi в интервалы j: pj = Nj/N, где Nj – число значений Xi , попавших в интервал j;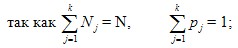 
- среднее значение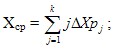 
- дисперсия (характеристика рассеивания)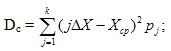 
- среднее квадратическое отклонение σc= - коэффициент вариации Vc=σc/Xcp График статистического распределения, называемого гистограммой, приведен на рис. 3.5 а. Если увеличивать число N и сокращать размер разрядов ΔX, разрядная частость стремится к плотности вероятности непрерывной случайной величины x. Плотность вероятности - вероятность появления какого-либо значения x: q(x)=lim pj при ΔX → 0 Характеристики плотности вероятности подобны статистическим характеристикам гистограммы цифрового массива:
- математическое ожидание x :
- дисперсия:
- среднее квадратическое отклонение: σ= - коэффициент вариации: V=σ/xмо На стадии проектирования, в первом приближении, можно рассчитать параметры случайного распределения напряжение из условия его подчинения нормальному закону. Случайная величина х нормально распределена, если ее плотность распределения имеет вид: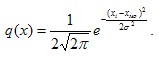 
Свойство нормального закона (рис. 4.4 б): 
Рис. 3.5. а) Гистограмма распределения с шагом квантования ΔX и плотность вероятности случайной величины х. б) Нормальный закон распределения и гистограмма нагрузки с шагом квантования 2σ, распределение которой подчиняется нормальному закону. в) График нагрузки, отрабатывающий нормальный закон. Таблица 3.4 Свойства нормального закона распределения и сформированной на нем гистограммы нагрузок (рис. 3.5 б)
В таблице Тном – нагрузка или напряжение номинальные или средние, рассчитанные в п. 3.1.1. После конвертации гистограммы нагрузок, сформированной на нормальном законе распределения, получится трехступенчатый график нагрузки (крутящий момент, сила в зацеплении, либо приложенная в любой точке детали), отрабатывающий нормальный закон, рис. 3.5 в: Таблица 3.5
Таблица 3.5 – это выписка из таб. 3.4, в которой среднее квадратическое значение нагрузки обозначено Тско . Это обозначение будет применяться в дальнейшем изложении, чтобы избежать одинакового обозначения среднего квадратического отклонения σ теории вероятностей и нормального напряжения σ сопротивления материалов. VТ = Тмо / Тско - коэффициент вариации нагрузки. Из механики разрушения материалов известно, что процесс развития трещин, накопления усталостного повреждения и ресурс детали зависит от уровня действующих напряжений. В п. 3 показана прямая пропорциональная связь между нагрузками и напряжениями. Отсюда следует, что вероятность возникновения напряжения σ(Т), создаваемого нагрузкой Т такая же, как и для Т. Обозначив параметр Т графика нагрузки напряжением σ, получим характеристики напряжения: Таблица 3.6
В таблица 3.6 : Если средние нагрузки и напряжения рассчитываются на основании исходных данных проекта (п. 3.1.1), то для определения средних квадратических отклонений может служить статистика коэффициентов динамичности, характерных для различных рабочих органов и механизмов. Коэффициент динамичности может быть выражен через нагрузку или через созданное нагрузкой напряжение в детали: Кд = (Тст + Тдин) / Тст = 1 + Тдин / Тст , где
Тст– статическая нагрузка, которая есть среднее значение всякого динамического процесса; Для нагрузок машин в установившемся режиме с постоянной скоростью движения характеристикой динамики колебаний нагрузки относительно среднего значения является среднее квадратическое отклонение динамического процесса. Тогда Кд = 1 + Тско / Тср = 1 + VТ При наличии достоверных данных о максимальных коэффициентах динамичности (7, 8), полученных на основе длительных наблюдений, можно полагать, что максимальные динамические нагрузки, характеризуемые как «кратковременные перегрузки» достигшие величины 3Тско при вероятности возникновения не более (1-0,997)/2 = 0,0015 (рис. 3.4). Тогда Кд макс = 1 + 3Тско / Тср = 1 + 3VТ , Коэффициент вариации нагрузки на деталь VТ и равные им коэффициенты вариации напряжений той же детали Vσ найдем: VТ = Vσ = (Кд макс – 1) / 3. После расчета (п. 4.1.1) средних значений, средние квадратические значения будут: Тско = Тср VТ и σско= σср Vσ (3.4) Статистика коэффициентов динамичности для технологического оборудования и полученные на их основе коэффициенты вариации нагрузок и вызываемых ими напряжений в таб. 3.7. Для получения коэффициентов вариации использованы максимальные значения коэффициентов динамичности из приведенных диапазонов Кд. Таблица 3.7. Характеристики динамики технологических машин и механизмов.
Коэффициенты вариации крутящих моментов в трансмиссиях сельскохозяйственных машин в зависимости от механизма и режима работы изменяются в еще более широких пределах по данным полевых испытаний:
Данные по испытаниям комбайнов, проведенные кафедрой ОКМ в приложениях, таб. П.12, П.13. |
;
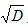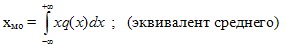
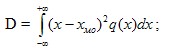
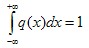- полная площадью под кривой плотности распределения q(x) характеризует все время возникновения случайной величины, за которое x может принять значения от -∞ до +∞. Если ограничить величину x значениями от xмо - 3 σ до xмо + 3 σ, то площадью под q(x) составит 0,997, т.е. появление ограниченных значений x произойдет за 0,997 от всего времени возникновения x. Части площади под нормальным распределением q(x), соответствующие характерным значениям x приведены в таблице 3.4.
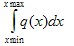
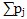или доля времени ti действия нагрузок