

|
Вопрос истечения жидкости через отверстия является одним из основных Механики жидкости и газа. Ученые и инженеры изучали этот вопрос, начиная с XVII в. Уравнение Д. Бернулли впервые было выведено при решении одной из задач истечения жидкости из отверстия. При расчетах диафрагм, дырчатых смесителей, наполнении и опорожнении резервуаров, бассейнов, водохранилищ, шлюзовых камер и других емкостей решаются задачи истечения жидкостей через отверстия. При решении этих задач определяют скорости и расходы жидкостей.
Ниже приведены основные определения, характеризующие процесс истечения жидкости через отверстия и насадки.
Отверстие называется малым, если напор во всех его точках можно считать постоянным. Это условие с достаточной точностью выполняется, если диаметр отверстия значительно меньше высоты столба жидкости от оси отверстия до свободной поверхности .
Истечение называется с совершенным сжатием, если на процесс истечения не оказывают влияние боковые стенки сосуда. Это условие выполняется при их удалении от отверстия на расстояние более трех диаметров.
Если с одной или нескольких сторон это расстояние, меньшее трех диаметров отверстия, то имеет место неполное сжатие поперечного сечения струи.
Если стенки удалены по периметру на расстояние меньше трех диаметров, то истечение называется с несовершенным сжатием.
Степень сжатия оценивается коэффициентом сжатия: 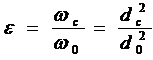 Эффект сужения истекающей струи проиллюстрирован на рис.1: а) для истечения через отверстие в тонкой стенке толщиной ; б) для истечения через отверстие с кромкой обратной конусности. 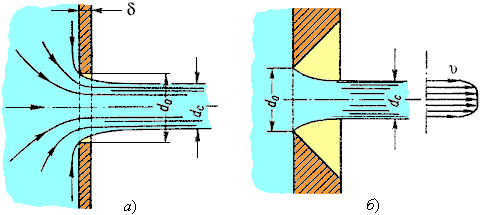
Таким образом, коэффициент сжатия - это отношение площади живого сечения струи в сжатом сечении к площади отверстия. Применение уравнения Бернулли позволяет выразить: 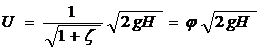 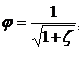 В случаях идеальной жидкости скорость струи равна теоретической: 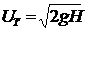 Следовательно коэффициент скорости представляет собой отношение действительной скорости жидкости в струе к теоретической. Расход жидкости определяется, как произведение скорости истечения на фактическую площадь сечения: 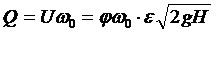 Произведение коэффициентов скорости и сжатия принято называть коэффициентом расхода: 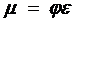 Тогда: 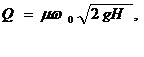 Тогда теоретический расход равен: 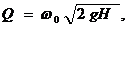 коэффициент расхода есть отношение действительного расхода к теоретическому: 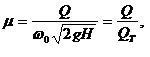 Коэффициент сжатия, скорости, расхода и сопротивления зависят от типа отверстия или насадка и от критерия Рейнольдса: 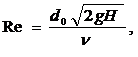 Насадком называется патрубок (короткая трубка), длина которого равна нескольким диаметрам d0. а)

б) 
в) 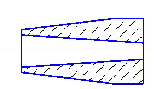
г) 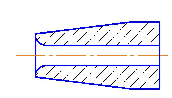 Рис.2 - Основные виды насадков Насадки делятся на три основные группы: цилиндрические, конические и коноидальные. Цилиндрические насадки (рис. 2, а) разделяют на внешние и внутренние. Конические насадки разделяют на сходящиеся (рис.2, б) и расходящиеся (рис. 2, в), их осевые сечения представляют собой усеченные конусы. Коноидальные (рис.2, г) насадки имеют воронкообразную входную часть, выполненную по форме вытекающей струи, а выходной участок – цилиндрический. При истечении через отверстия/насадки, можно наблюдать как струя во время полета не сохраняет форму живого сечения отверстия (рис.3). 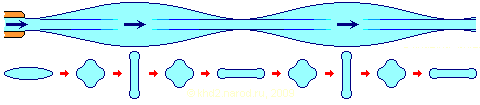 Рис.3 - Периодическое изменение инверсии струи. На рис.3а показан идеализированный псевдоспиральный вид струи с периодической инверсией, истекающей из узкого овального отверстия, внизу (рис.3б) - сечения этой струи на разных расстояниях от отверстия. |
