4. Краткие методические указания к выполнению расчетов
4.2. Кинематический расчет манипулятора
Эта часть расчетов требует определения функции положения, скорости и ускорения характерных точек манипулятора в пространстве обобщенных координат. Эти расчеты необходимы для составления уравнений движения. К характерным точкам относятся центр захватного устройства и центр тяжести 3-го звена. Функцию положения определяют векторно–матричным методом Денавита–Хартенберга. Для этого составляют таблицу параметров звеньев и кинематических пар, матрицы переходов от системы координат i–го звена к системе координат (i-1)-го звена и к абсолютной системе координат. Определяют абсолютные координаты центра схвата и центра масс 3-го звена, а также максимальные ускорения для каждой обобщенной координаты. Векторное уравнение для схвата:
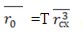 , ,
где Т- матрица перехода; 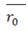 - вектор схвата в абсолютной системе координат; - вектор схвата в абсолютной системе координат;
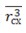 - вектор схвата в системе координат схвата. - вектор схвата в системе координат схвата.
Максимальные ускорения обобщенных координат определяются из анализа графика изменения скорости при разгоне и торможении.[7,кн. 3,с.94-95]. Принимают, что закон изменения скорости трапецеидальный
 , ,
где 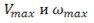 , ,
- линейная и угловая скорости из задания;
tp = 0,13t - время разгона, с; где t - время перемещения звена по координате.
Время t находим из выражений:
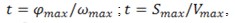 , ,
где 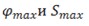 - максимальные угол и путь перемещения звена по координате. - максимальные угол и путь перемещения звена по координате.
Коэффициент ускорения Ka у современных роботов с электроприводом Ka = 1,5-2,5 , с пневмоприводом принимать Ка = 2,0-2,5. Далее определяем скорость схвата в абсолютной системе координат [7, кн. 1, с. 100-102]
 , ,
где 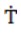 - производная матрицы перехода по времени. - производная матрицы перехода по времени.
Производную 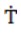 находим из выражения [7, кн. 1., с. 92] находим из выражения [7, кн. 1., с. 92]
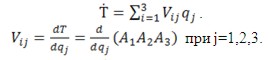
Ускорение схвата в абсолютной системе координат определяют в соответствии с формулой (3.42) [7, кн. 1., с. 101].
|



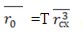 ,
,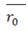 - вектор схвата в абсолютной системе координат;
- вектор схвата в абсолютной системе координат;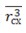 - вектор схвата в системе координат схвата.
- вектор схвата в системе координат схвата.  ,
,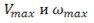 ,
,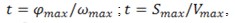 ,
,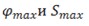 - максимальные угол и путь перемещения звена по координате.
- максимальные угол и путь перемещения звена по координате. ,
,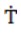 - производная матрицы перехода по времени.
- производная матрицы перехода по времени.