|
1.1.1. Распределение Стьюдента (t-критерий).
Распределение было получено Госсетом (псевдоним Стьюдента) в 1908 г. Зависит от объема выборки N или числа степеней свободы 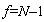 , с которым определена выборочная дисперсия , с которым определена выборочная дисперсия 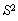 (среднее квадратическое отклонение (СКО) выборки S), и от заданной вероятности ответа, определяемой параметром уровня значимости q . Формула критерия: (среднее квадратическое отклонение (СКО) выборки S), и от заданной вероятности ответа, определяемой параметром уровня значимости q . Формула критерия:
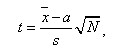
где а — генеральное среднее исследуемой случайной величины 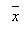 — выборочное математическое ожидание X.
— выборочное математическое ожидание X.
Распределение симметрично относительно начала координат, т. е. 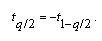 . .
Более полные таблицы квантилей распределения Стьюдента для уровня значимости 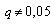 содержатся в [1]. содержатся в [1].
Таблица 1
Квантили распределения Стьюдента при q=0,05
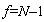 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 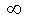 |
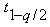 | 12,71 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,37 | 2,31 | 2,26 | 2,23 | 2,09 | 2,04 | 1,96 |
Распределение Стьюдента дает возможность находить генеральное среднее или проверять статистические гипотезы при очень малых выборках.
Пример 1. Известны три значения нормально распределенной случайной величины X: 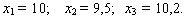 Требуется оценить генеральное среднее с вероятностью р = 0,95 (задача первого типа).
Определим выборочное (N = 3) математическое ожидание
Требуется оценить генеральное среднее с вероятностью р = 0,95 (задача первого типа).
Определим выборочное (N = 3) математическое ожидание 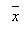
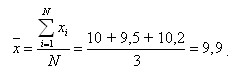
Определим выборочное СКО при f = N–1=2:
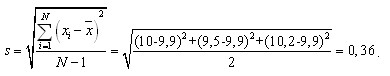
Запишем выражение для t в соответствии с (1): 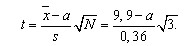
По табл. 1 определим квантильные границы 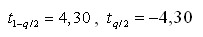 и запишем неравенство и запишем неравенство 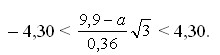
Решив неравенство относительно а, получим с доверительной вероятностью р = 0,95
9,0 < а < 10,8.
Пример 2. Проверить гипотезу, состоящую в том, что нормально распределенная случайная величина Х имеет генеральное математическое ожидание а = 10 на основании результатов двух испытаний: 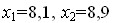 (задача второго типа). (задача второго типа).
По результатам испытаний определяем 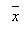 =8,5 и s = 0,57.
Вычисляем по (1) значение критерия Стьюдента t: =8,5 и s = 0,57.
Вычисляем по (1) значение критерия Стьюдента t: 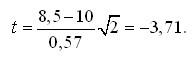 Выбираем уровень значимости q = 0,05 и по табл. 1 находим для
f=N–1=1 границы критических областей гипотезы
Выбираем уровень значимости q = 0,05 и по табл. 1 находим для
f=N–1=1 границы критических областей гипотезы 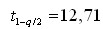 , , 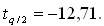
Гипотеза не отвергается на уровне значимости q=0,05, поскольку
t = –3,71 лежит вне критических областей. Отметим, что очень малая информация (N = 2) и низкий уровень значимости не дают оснований отвергнуть плохую на взгляд гипотезу. Если бы, например, те же результаты ( 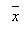 = 8,5 и s = 0,57) были получены при N = 4 (f = 3), то, как легко видеть, гипотезу следовало отвергнуть на том же уровне значимости. При выборе более жесткого уровня значимости, = 8,5 и s = 0,57) были получены при N = 4 (f = 3), то, как легко видеть, гипотезу следовало отвергнуть на том же уровне значимости. При выборе более жесткого уровня значимости, 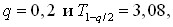 т. е. гипотеза также должна быть отвергнута. т. е. гипотеза также должна быть отвергнута.
|



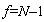 , с которым определена выборочная дисперсия
, с которым определена выборочная дисперсия 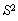 (среднее квадратическое отклонение (СКО) выборки S), и от заданной вероятности ответа, определяемой параметром уровня значимости q . Формула критерия:
(среднее квадратическое отклонение (СКО) выборки S), и от заданной вероятности ответа, определяемой параметром уровня значимости q . Формула критерия:
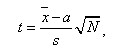
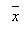 — выборочное математическое ожидание X.
— выборочное математическое ожидание X.
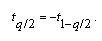 .
.
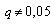 содержатся в [1].
содержатся в [1].
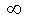
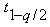
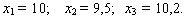 Требуется оценить генеральное среднее с вероятностью р = 0,95 (задача первого типа).
Определим выборочное (N = 3) математическое ожидание
Требуется оценить генеральное среднее с вероятностью р = 0,95 (задача первого типа).
Определим выборочное (N = 3) математическое ожидание 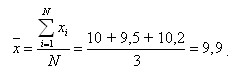
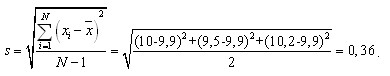
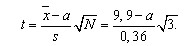
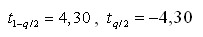 и запишем неравенство
и запишем неравенство 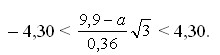
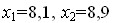 (задача второго типа).
(задача второго типа).
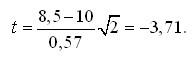 Выбираем уровень значимости q = 0,05 и по табл. 1 находим для
f=N–1=1 границы критических областей гипотезы
Выбираем уровень значимости q = 0,05 и по табл. 1 находим для
f=N–1=1 границы критических областей гипотезы 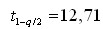 ,
, 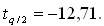
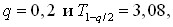 т. е. гипотеза также должна быть отвергнута.
т. е. гипотеза также должна быть отвергнута.