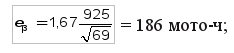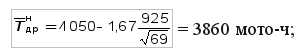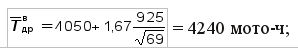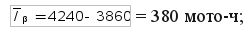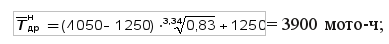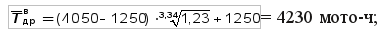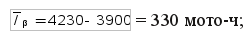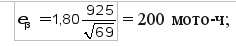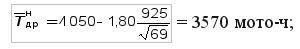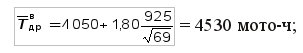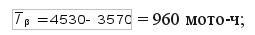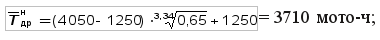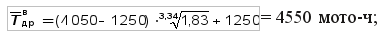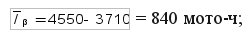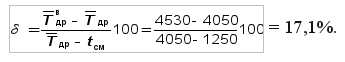В результате испытания (наблюдения) группы машин и обработки собранной при этом информации определяют количественные характеристики показателей надежности (среднее значение В дальнейшем значения этих характеристик должны быть перенесены (запланированы) на другие группы машин, работающие в других условиях. Естественно, что изменение количества машин в группе и условий их эксплуатации вызовет изменение количественных характеристик показателя надежности. При расчете доверительных границ рассеивания показателей надежности (ГОСТ 17510 – 72) рекомендуется применять следующие значения доверительных вероятностей: β = 0,80; 0,90; 0,95; 0,99. Инженерные расчеты рассеивания одиночного показателя надежности проводят при планировании сроков постановки отдельных машин или их агрегатов в ремонт, при определении остаточного ресурса деталей и сопряжений по данным микрометража и т. д., т. е. тогда, когда определяют характеристики показателя надежности одной машины. На практике чаще приходится встречаться с расчетом доверительных границ среднего значения показателя надежности
Для определения доверительных границ рассеивания среднего значения показателя надежности, при законе нормального распределения и заданной доверительной вероятности a вначале находят абсолютную ошибку еβ
где tβ – коэффициент Стьюдента, определяется по табл. V приложения. Нижняя доверительная граница
где Верхняя доверительная граница
Доверительный интервал
Из теории надежности известно, что сложение нескольких одинаковых или различных теоретических законов распределения приводит в итоге к закону нормального распределения. Поэтому, когда рассеивание одиночных показателей надежности подчинено закону распределения Вейбулла, рассеивание средних значений ПН в таких случаях согласуется с законом нормального распределения. Следовательно, доверительные границы рассеивания среднего значения при ЗРВ можно определять по уравнениям (31) и (32). Однако, когда требуется повышенная точность определения, доверительные границы рассеивания среднего значения
где r1 и r3 – коэффициенты распределения Вейбулла, определяемые по табл. V приложения в зависимости от заданной величины доверительной вероятности β и повторности информации N. При расчетах характеристик показателя надежности и переносе их на другие группы машин той же марки необходимо оценивать наибольшую возможную ошибку такого переноса. Наибольшая абсолютная ошибка переноса опытных характеристик показателя надежности при заданной доверительной вероятности будет равна по величине еβ в обе стороны от среднего значения ПН. Для удобства расчета относительную предельную ошибку δ определяют в процентах от среднего значения показателя надежности
Относительную ошибку переноса определяют всегда при односторонней доверительной вероятности β0. Задача 4. Проведены испытания 69 новых двигателей (число задается в соответствии с вариантом табл. 3); установлено, что рассеивание их доремонтного ресурса подчинено закону нормального распределения с параметрами Требуется определить, в каких пределах может измениться их средний доремонтный ресурс, если вновь провести испытания таких же 69 двигателей? Для решения задачи задаемся доверительной вероятностью β = 0,90 (в соответствии с вариантом табл. 3) и определяем коэффициент Стьюдента tβ = 1,67 (табл. V приложения). По уравнениям (30) – (33) рассчитываем доверительные границы рассеивания среднего доремонтного ресурса двигателя: — для нормального закона распределения: абсолютная ошибка нижняя доверительная граница
верхняя доверительная граница
доверительный интервал
— для закона распределения Вейбулла (b = 3,34; tсм = 1250 мото-ч), задавшись β = 0,90, по табл. V приложения определим: r1 = 1,23; r3 = 0,83 по формулам (34) и (35): нижняя доверительная граница
верхняя доверительная граница
доверительный интервал
В отличие от доверительных границ при законе нормального распределения доверительные границы при законе распределения Вейбулла асимметричны среднему значению показателя надежности Например, при расчете среднего доремонтного ресурса двигателя для N = 69 и β0 = 0,90 относительная ошибка переноса может достигать предельной величины:
Задача 5. В хозяйстве одновременно работают N0 = 12 новых двигателей той же марки (N0 выбирается в соответствии с вариантом табл. 3). В каких пределах следует учитывать возможные изменения среднего доремонтного ресурса при планировании их загрузки, если известны результаты испытания 69 двигателей этой марки? Для решения задачи задаемся; доверительной вероятностью β = 0,90 (в соответствии с вариантом табл. 3) и определяем коэффициент Стьюдента tβ = 1,80 (табл. V приложения). По уравнениям (30) – (33) рассчитываем доверительные границы рассеивания среднего доремонтного ресурса двигателя: — для нормального закона распределения: абсолютная ошибка
нижняя доверительная граница
верхняя доверительная граница
доверительный интервал
— для закона распределения Вейбулла (b = 3,34; tсм = 1250 мото-ч), задавшись β = 0,90 и N =12, по табл. V приложения определим: r1 = 1,73; r3 = 0,65 по формулам (34) и (35): нижняя доверительная граница
верхняя доверительная граница
доверительный интервал
относительная ошибка переноса может достигать предельной величины:
Доверительные границы у доремонтного ресурса двигателя вследствие меньшего количества машин в хозяйстве (N = 12) будут шире, чем при N = 69. |

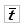 , среднее квадратическое отклонение S и др.).
, среднее квадратическое отклонение S и др.).

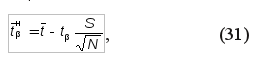


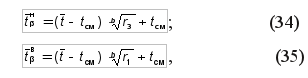
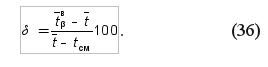
 = 4050 мото-ч и S = 925 мото-ч.
= 4050 мото-ч и S = 925 мото-ч.