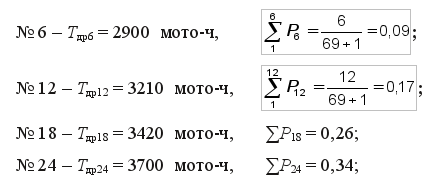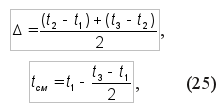Достоинство метода вероятностной бумаги — возможность обработки всех видов информации: полной, усеченной и многократно усеченной. Кривая накопленных опытных вероятностей или интегральная кривая теоретического закона распределения (см. рис. 2) носит естественно криволинейный характер. По внешнему виду этой кривой трудно определить, какому закону подчиняется рассеивание показателя надежности, и невозможно определить параметры этого закона. Кроме того, в случае усеченной информации и известного закона распределения на такой график удается нанести только начальные точки информации. Функциональную сетку вероятностной бумаги составляют так, чтобы нанесенная на эту бумагу интегральная функция распределения была представлена прямой линией (интегральная прямая). Затем на функциональную сетку вероятностной бумаги наносят все или выбранные (i-е) точки исходной информации в соответствии с их координатами: абсциссой (величина показателя надежности ti) и ординатой (величина накопленной опытной вероятности ∑Рi). При использовании вероятностной бумаги для выбора теоретического закона распределения (ЗНР или ЗРВ) отпадает необходимость в предварительном расчете характеристик показателя надежности Расчет показателя надежности начинается с выбора из таблицы исходной информации опытных точек для их нанесения на функциональную сетку вероятностной бумаги. При незначительной повторности (N < 10) используют все точки информации. Для упрощения построений и последующих расчетов ПН при N > 10 рекомендуется из общего количества информации выбирать 5 — 7 точек, равномерно расположенных, в общем ее объеме. При этом накопленная вероятность первой выбранной точки должна находиться в пределах ∑Р1 = 0,08 — 0,15, а последняя выбранная точка должна быть последней (i = N) или предпоследней (i = N – 1) точкой исходной информации. Учитывая, что многие ПН тракторов и сельскохозяйственных машин имеют смещение tcм (дополнительная точка информации), накопленную вероятность выбранных точек определяют по уравнению:
где № i — порядковый номер i-й точки в таблице исходной информации. Задача 2. Определить параметры теоретического закона распределения (ТЗР) безотказной работы двигателей при обработке усечённой информации. Предположим, что наблюдение за двигателями велись по плану NUТ (наблюдения ведутся за N машинами до наперед заданной наработки Т независимо от того, у скольких машин из числа N будут зарегистрированы показатели надежности), где Т = 4200 мото-ч. Тогда в период наблюдения предельные состояния (ресурсные отказы) были бы зафиксированы у 36 двигателей (N0 = 36, при решении задачи выбирается в соответствии с вариантом по табл. 3) из общего количества испытываемых двигателей (N = 69) (см. табл. 5). Для нанесения на вероятностную бумагу из усеченной таким образом информации выбираем шесть (5 – 7) равномерно расположенных точек: № 6, 12, 18, 24, 30 и 36. Координаты этих точек будут соответственно равны [см. табл. 1 и уравнение (23)]:
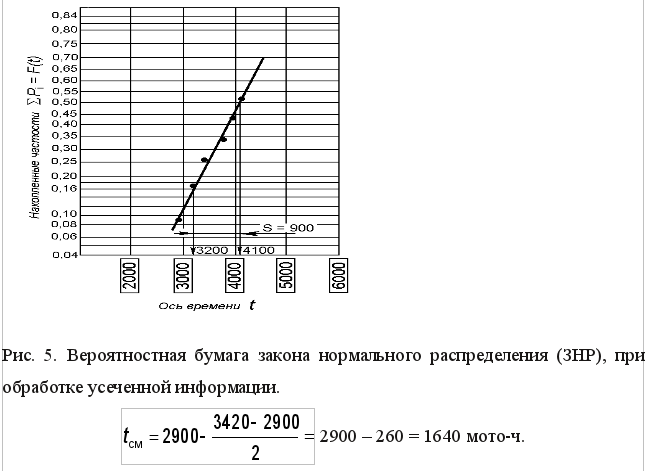
По полученным данным строятся интегральные прямые с использованием вероятностной бумаги и определяются параметры закона распределения. Для закона нормального распределения (ЗНР) (рис. 5): – среднее значение показателя надежности
– значение среднего квадратического отклонения S равно разности абсцисс точек с ординатами F(t) = 0,5 ( S = – коэффициент вариации V для ЗНР определим по формуле (9):
где tсм – величина смещения, при незначительном количестве информации (N < 25) и отсутствии статистического ряда определяется по формуле: tсм = t1 – Δ, (24) где Δ — среднее значение разностей первых трех-четырех значений ПН.
где t1 = 2900, t2 = 3210, t3 = 3420 мото-ч – значения соответственно 1, 2 и 3-го ПН в порядке их возрастания.
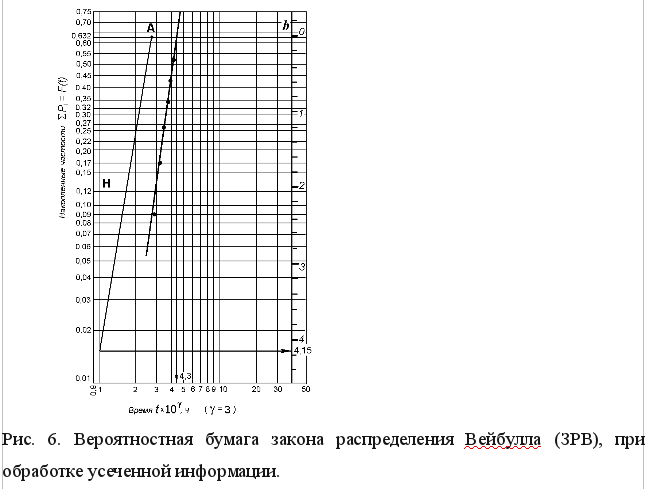
Для закона распределения Вейбулла (ЗРВ) (рис. 6):
a = t – tсм, (26) где t — определяется как абсцисса точки пересечения интегральной прямой с ординатой F(t) = 0,632: t = 4,3·10γ = 4,3·103 = 4300 мото-ч; γ = 3 масштаб оси времени, выбирается так, чтобы интегральная прямая попала в середину вероятностной бумаги. Следовательно а = 4300 – 1640 = 2660 мото-ч. Если используется вариационный ряд (табл. 1), то tсм = = 1150 мото-ч. и а = 4300 – 1150 = 3150 мото-ч. Параметр формы b определяют как ординату (по оси b) точки пересечения вертикальной прямой Н и прямой, проведенной параллельно интегральной, через точку А
Коэффициент вариации V для ЗРВ определяется по табл. II приложения в зависимости от параметра b. Если b = 4,15, то V = 0,272. |

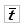 , S и V.
, S и V.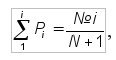 (23)
(23)