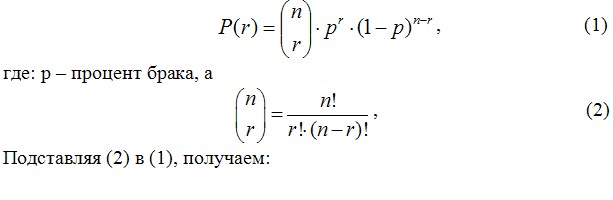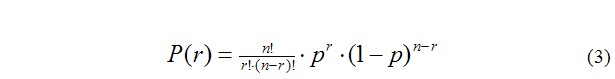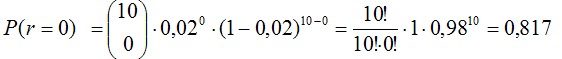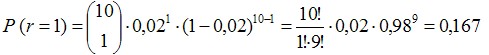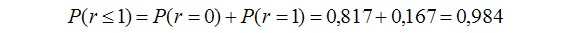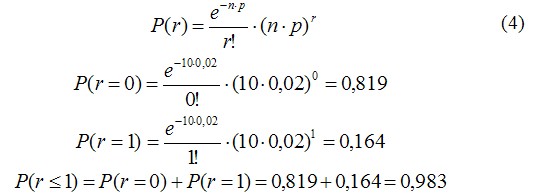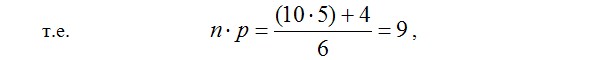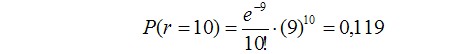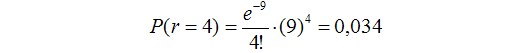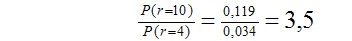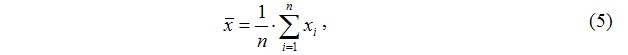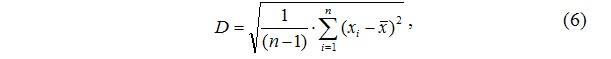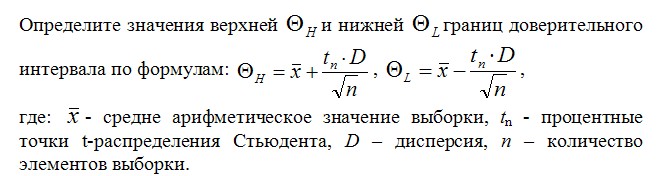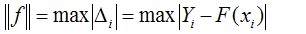1. Пояснительная записка

Дисциплина предназначена для развития будущим технологам в области машиностроительного производства навыков использования в практической деятельности современных систем компьютерного моделирования и анализа сложных технических систем.
По завершении изучения дисциплины студент должен знать: место и роль методов математической статистики в решении производственных задач, как определяются числовые характеристики выборок, какие существуют законы распределения случайных величин и как они используются в промышленности при решении производственных задач, как определяется необходимый объем выборки для получения заданного доверительного интервала, какими методами решается задача аппроксимации функций, а также назначение и основные функциональные возможности современных программных средств математического моделирования.
Студент должен уметь: оценивать вероятности получения требуемого результата при решении производственных задач, выполнять статистический анализ результатов промышленного эксперимента вручную и средствами системы MathCAD, строить и анализировать функциональные модели процессов функционирования технических систем, идентифицировать регрессионную модель первого и второго порядка, исследовать ее на оптимальность средствами системы MathCAD.
Пререквизиты: математика, физика, теоретическая механика, инженерная графика, научные основы технологии машиностроения, информатика, математическое моделирование в технологии машиностроения.

2. Содержание дисциплины

Приложения статистики в задачах моделирования. Выборка из совокупности как источник получения числовых оценок параметров модели.
Числовые характеристики выборок. Характеристики положения. Характеристики рассеяния (разброса). Случайные величины и функции их распределения. Свойства функции распределения. Плотность распределения. Математическое ожидание случайной величины. Дисперсия случайной величины [1-7].Важнейшие дискретные распределения и их использование в промышленности. Биномиальное распределение. Распределение Пуассона. Задачи оценивания процента брака, производственного травматизма, моделирования отказов при испытаниях, решаемые с помощью дискретных распределений. Важнейшие непрерывные распределения. Равномерное распределение. Нормальное (Гауссово) распределение. t-распределение Стьюдента.
Подбор распределения по экспериментальным данным, полученных на производстве. Использование непрерывных распределений в задачах моделирования достижения точности [1-7].Оценивание с помощью доверительных интервалов. Понятие доверительного интервала. Построение доверительных интервалов для исследования характеристик совокупностей по выборкам, полученных при проведении промышленного эксперимента. Определение необходимого объема выборки для получения доверительного интервала заданного размера. Исключение выбросов. Об ошибках косвенных измерений [2, 7].Случайные процессы. Основные понятия случайных процессов. Корреляционная функция случайного процесса.
Стационарность и эргодичность случайного процесса. Шероховатость поверхности как эргодичный стационарный процесс [2, 7].Функциональные модели процессов. Функциональная модель и этапы ее создания. Регрессионные модели. Понятие регрессии. Примеры линейной и нелинейной регрессии. Применимость регрессионных моделей (на примере однофакторной линейной регрессии) в промышленных задачах.
Идентификация функциональной модели как задача аппроксимации. Приближение эмпирических данных, полученных в производстве и задача аппроксимации функций. Понятие нормы функции. Идентификация по методу наименьших квадратов.
Идентификация по Чебышёву. Методы минимизации нормы ошибки идентификации, используемые в промышленных задачах. [1- 3].

3. Исходные данные для выполнения контрольной работы
Задание №1

В зависимости от варианта задания, представленного в нижеприведённой таблице решить одну из двух задач:
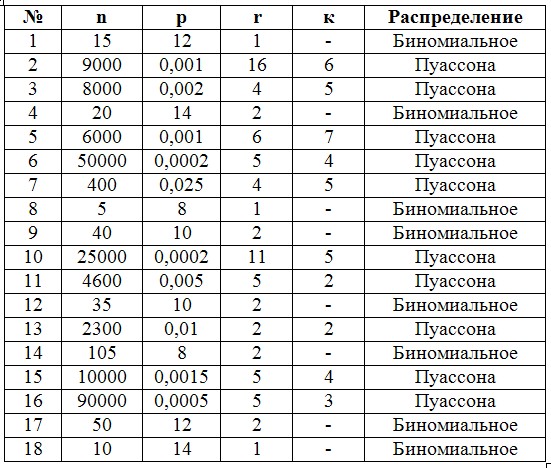
1.Пусть в некотором процессе получается p% брака. Берется выборка из n независимых образцов. С помощью биномиального распределения найдите вероятность того, что в этой выборке будет не более, чем r бракованных образцов.
2. Предприятие выпустило n оптических приборов за к лет. В среднем, количество отказов этих приборов составила n*p штук в год. После внесения изменений в конструкцию прибора, в течение следующего года предприятию вернули всего r дефектных прибора. С помощью распределения Пуассона оцените вероятность появления числа дефектных приборов после изменения конструкции и оцените, во сколько раз вероятность этого события меньше (больше) вероятности до изменения конструкции?

Задание № 2

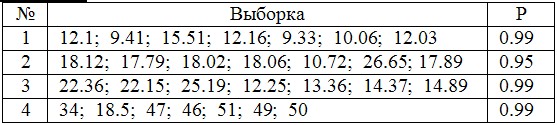
В предложенной выборке исключите возможные выбросы и найдите доверительный интервал для среднего. Доверительная вероятность P

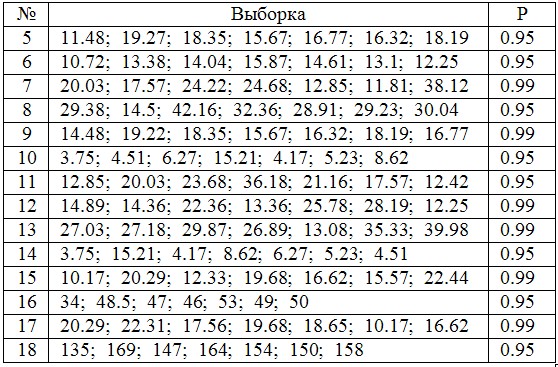
Задание №3

Совокупность измеренных размеров деталей подчинена нормальному распределению с параметрами μ (мм), σ(мм). Оцените количество деталей в заданном допуске в выборке из n деталей.

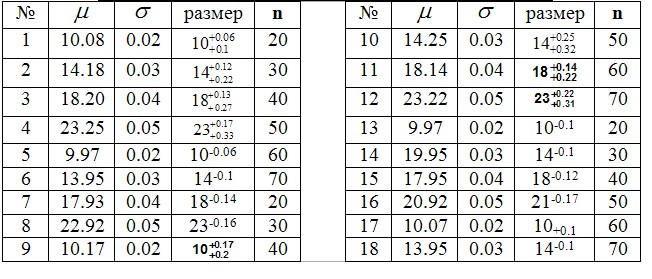
Задание №4

Для последовательности экспериментальных точек определите нормы погрешности приближения функции y=f(x) по Гауссу и Чебышеву.

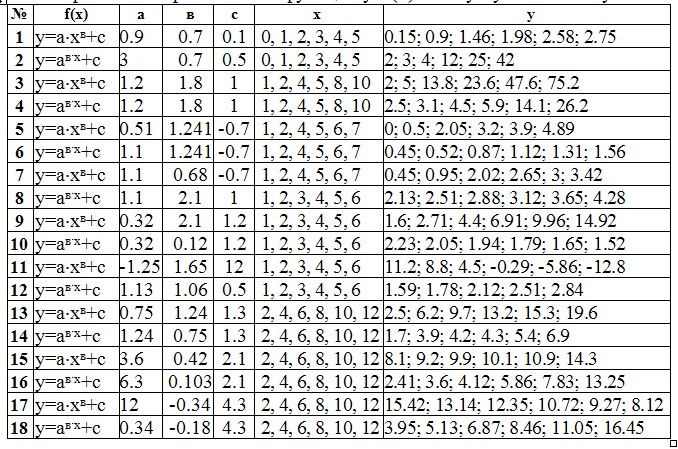
4. Методика выполнения заданий контрольной работы
4.1. Определение вероятности события, с использованием биномиального распределения и распределения Пуассона.

4.1.1. Вероятность события, при котором в выборке (n – количество элементов выборки) будет присутствовать определенное количество бракованных образцов (r – количество бракованных образцов) определяется по формуле:


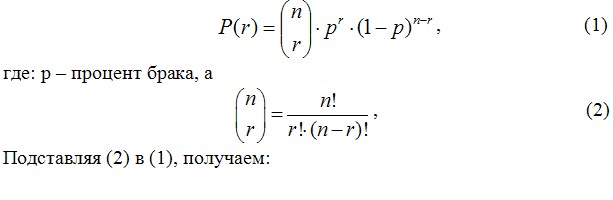
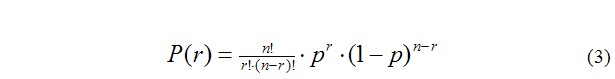
Рассмотрим пример использования биноминального распределения и распределения Пуассона в практических задачах.
Задание 1: Пусть в некотором процессе получается 2% брака. Берется выборка из 10 независимых образцов. Найти вероятность того, что в этой выборке не окажется дефектов; будет не более чем один дефект.
Решение:
Вероятность того, что в этой выборке не окажется бракованных образцов определяется по формуле:

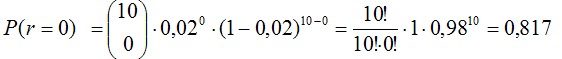
Вероятность того, что в этой выборке окажется только 1 бракованный образец определяется по формуле:

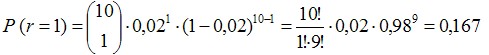
Ответ: Вероятность наличия в партии не более одного дефектного образца:

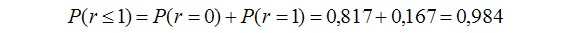
Оценим теперь вероятность того, что в этой выборке не окажется бракованных образцов с помощью распределения Пуассона и сравним полученный результат с биноминальным распределением по формуле:

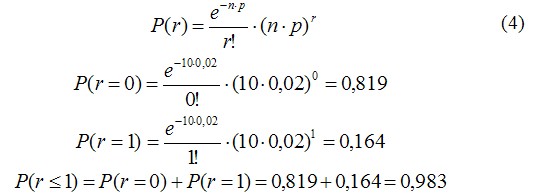
Сравнивая полученные результаты по биномиальному распределению и по распределению Пуассона видим, что значения вероятностей практически совпадают, однако вычисления по распределению Пуассона - проще.
Рассмотрим другой пример решения задачи с использованием распределения Пуассона.
Задание 2: Предприятие выпустило 150000 оптических приборов за 5 лет. В среднем, количество отказов этих приборов составила 10 штук в год. После внесения изменений в конструкцию прибора, в течение следующего года предприятию вернули всего 4 дефектных прибора. С помощью распределения Пуассона оцените вероятность появления числа дефектных приборов после изменения конструкции и оцените, во сколько раз вероятность этого события меньше (больше) вероятности до изменения конструкции?
Решение:
Поскольку математическое ожидание (среднее число) дефектных приборов определяется постоянной величиной произведения ,

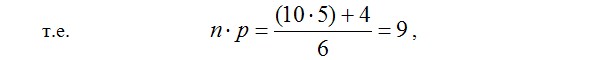
то вероятность числа дефектных приборов до изменения конструкции составила:

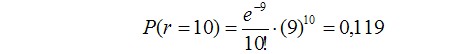
А вероятность появления числа дефектных приборов после изменения конструкции составила:

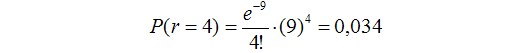
Оценим, во сколько раз вероятность снижения числа дефектных приборов после изменения конструкции меньше вероятности до изменения конструкции:

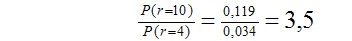
Таким образом, вероятность появления числа дефектных приборов после изменения конструкции за текущий период (год) в 3,5 раза меньше вероятности появления дефектных изделий до изменения конструкции за тот же период, что говорит о вполне удовлетворительной эффективности внесённых изменений в конструкцию.
4.2. Для данной выборки значений выходного параметра процесса, полученной дублированием эксперимента при неизменных значениях управляющих факторов, исключить выбросы, определить числовые характеристики выборки, построить доверительный интервал для математического ожидания.
4.2.1. Определить наличие “выбросов” в представленной выборке и при наличии таковых исключить их из дальнейших расчетов.
Запишите все элементы выборки в порядке возрастания их значений. Определите величину критического значения для определения выброса по формуле r₁₀=x₂-x₁/ x_n-x₁, где: x₁, x₂, x_n – значения первого, второго и последнего элементов выборки, расположенных в порядке возрастания значений.
Сравните величину r₁₀ с критическим значением (таблица 1). В случае, если r₁₀ меньше критического значения - x₁ не является выбросом, а если r₁₀ больше критического значения - x₁ является выбросом и его необходимо исключить из дальнейших расчетов. Запишите все элементы выборки в порядке убывания их значений. Определите величину критического значения для определения выброса по формуле r₁₀=x₂-x₁/ x_n-x₁, где: x₁, x₂, x_n – значения первого, второго и последнего элементов выборки, расположенных в порядке убывания значений.
Таблица 1

Критические значения для проверки выбросов (экстремальное значение)

Сравните величину r₁₀ с критическим значением (таблица 1). В случае, если r₁₀ меньше критического значения - x₁ не является выбросом, а если r₁₀ больше критического значения - x1 является выбросом и его необходимо исключить из дальнейших расчетов.
4.2.2. Определить максимальное и минимальное значение выборки, моду, размах выборки и среднее арифметическое значение.
Определите минимальное и максимальное значение выборки x_(min) и x_(max).
Определите моду выборки – наиболее часто встречающееся значение выборки (обозначается ).
Определите размах выборки R=x_(max)-x_(min).
Определите среднее арифметическое значение выборки по формуле:

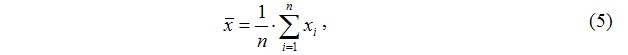
где: x_i – значения элементов выборки, n – количество элементов в выборке.
4.2.3. Определите выборочную дисперсию по формуле:

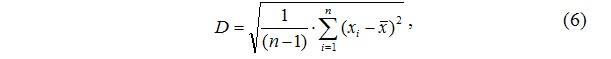
где: x_i – значения элементов выборки, n – количество элементов в выборке.
4.2.4. Определить значения верхней и нижней границ доверительного интервала для заданной доверительной вероятности.
Пользуясь таблицей 2, выпишите значение процентных точек t-распределения Стьюдента (t_{n =} ).
Таблица 2

Процентные точки t-распределения Стьюдента.

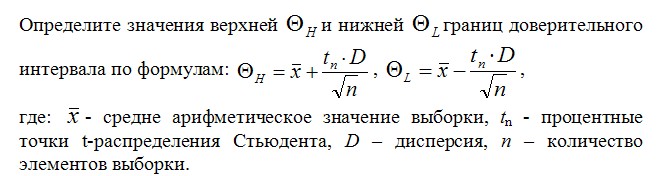
4.2.5. Отобразите на графике все элементы и характеристики выборки.
В результате проделанной работы все полученные величины необходимо нанести на график, имеющий следующий вид:

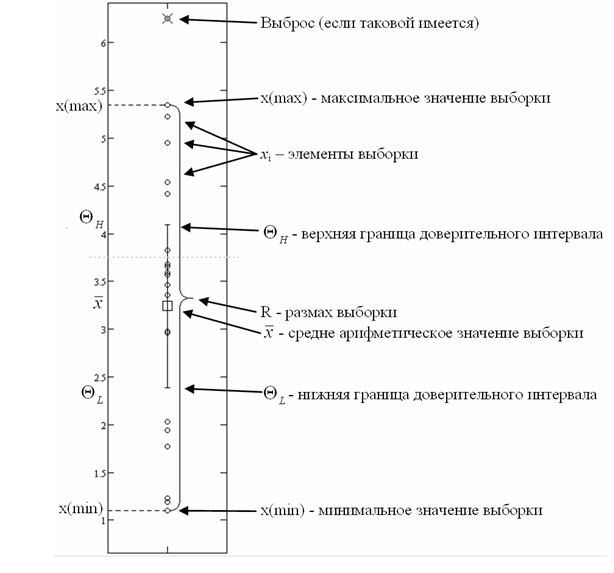
4.3. Используя закон нормального распределения, оцените количество бракованных деталей.
4.3.1. Преобразуйте размер детали к нормированной величине по формулам:

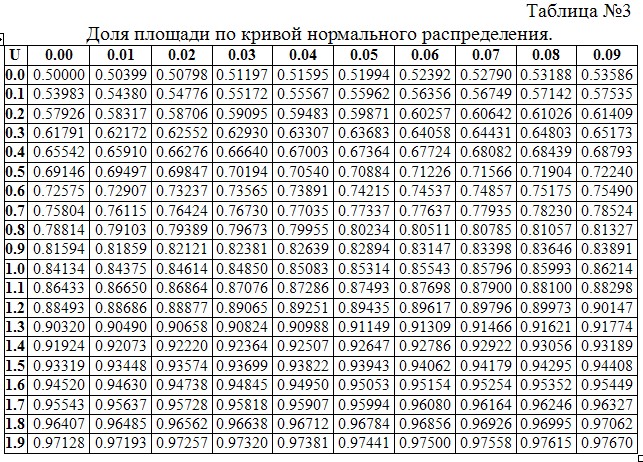
4.3.2. Используя табличные значения (таблица №3), определите площадь под кривой нормального распределения с учетом границ допуска на размер.
4.3.3. Оцените количество деталей, попавших и не попавших в поле допуска на размер.
Для решения 3-го задания рассмотрим пример.
Задание: Совокупность измеренных размеров деталей подчинена нормальному распределению с параметрами μ =10.02 мм, σ=0.03 мм. Оценить количество деталей в допуске 10.02+0.01 мм в выборке из 40 деталей.
Решение: 1.Преобразуем размер детали к нормированной величине U.

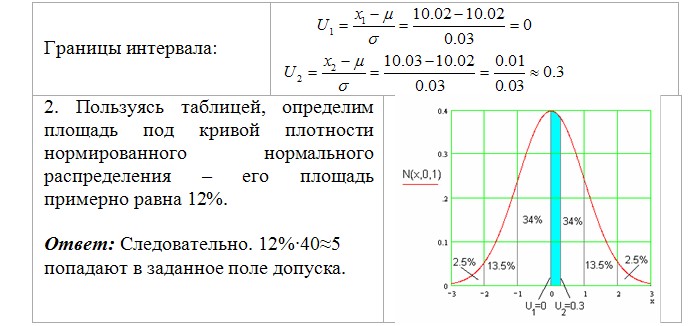
Примечание: Приведенные в таблице значения доли площади под кривой нормального распределения даны для размеров больших или равных математическому ожиданию. В случае, когда в ходе определения по формуле нормирования случайной величины Вы получили отрицательное значение, то реальная доля площади под кривой нормального распределения будет определяться как (1- значение таблицы без учета знака).

4.4. По заданной совокупности экспериментальных точек построить адекватную регрессионную модель и выполнить идентификацию ее параметров.
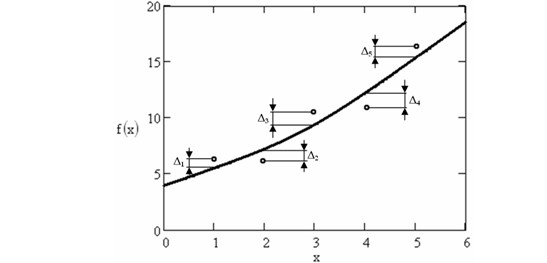
4.4.1. Определите значения функциональной модели при значениях абсциссы, соответствующих значениям абсциссы экспериментальных точек.
4.4.2. Определите значение “невязок” для каждой экспериментальной точки и функциональной модели по формуле Δ_i=Y_i- F(xi) , где: Y_i – значение ординаты экспериментальной точки в соответствии с заданием. F(xi) – значение уравнения Y= F(x_i) при значениях x_i, соответствующих значениям абсцисс экспериментальных точек.
4.4.3. Определите численное значение нормы Гаусса по формуле:

4.4.4. Определите численное значение нормы Чебышева по формуле

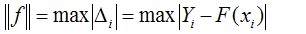
4.4.5. Постройте график, на котором нанесите функциональную модель, экспериментальные точки и рассчитанные в п. 4.4.2 “невязки”.



Литература.
1. Гмурман В.Е. Теория вероятностей и математическая статистика : Учеб. пособие для вузов / В. Е. Гмурман. - 9-е изд., стер. - М. : Высш. шк., 2003. - 479 с.
2. Мельников А.С., Шевцов С.Н. Математическое моделирование в технологии и проектировании. Интерактивный учебный курс http://de.dstu.edu.ru (http://static.dstu.edu.ru/aireng/ru/resources/metod%20razrab.html)
3. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике : Учеб. пособие для студентов вузов / В. Е. Гмурман. - 5-е изд., стер. - М. : Высш. шк., 1999. - 400 с. : ил.
4. Шакалис В.В. Моделирование технологических процессов.- М.: Машиностроение, 1973
5. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Т.1. Методы обработки данных., Т.2. Планирование эксперимента. М.: Мир, 1977
6. Вуколов, Э.А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXEL : учеб. пособие / Э. А. Вуколов. - 2-е изд., испр. и доп. - М. : Форум, 2008. - 463 с. : ил.
7. Хан Г., Шапиро С. Статистические модели в инженерных задачах.- М.: Мир, 1969.