Пересечение прямой с плоскостью

Прямая может принадлежать плоскости (см. §4), пересекать плоскость и быть параллельной ей. Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 30 приведен комплексный чертеж прямой l и плоскости треугольника ABC. Через горизонтальную проекцию прямой l₁ проводим проекцию вспомогательной горизонтально проецирующей плоскости Σ₁. Плоскость Σ пересекает плоскость треугольника АВС по прямой т. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ВС и АС со вспомогательной плоскостью Σ. Для получения фронтальной проекции линии m построим фронтальные проекции точек 1 и 2, соединив которые, получим фронтальную проекцию m₂.

В пересечении фронтальных проекций прямых т и l получим фронтальную проекцию точки К, принадлежащей и прямой l, лежащей в плоскости треугольника АВС и прямой т, лежащей в плоскости ?. Следовательно, точка К является точкой пересечения прямой l с плоскостью треугольника АВС.

Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3 и 4.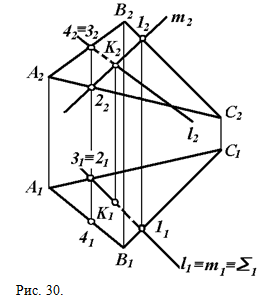

Если плоскость занимает частное положение, то одна проекция точки пересечения прямой с плоскостью определяется сразу в пересечении одной из проекций плоскости с соответствующей проекцией прямой (рис. 31, 32).

Если прямая пересекается с проеци¬рующей плоскостью, то точку пересече¬ния нужно только правильно отметить, ибо любая точка, принадлежащая проецирующей плоскости, будет проецироваться на соответствующий след проецирующей плоскости. Например, горизонтальная проекция К₁ точки пересечения К прямой АВ с горизонтально проецирующей плоскостью Р будет расположена на го¬ризонтальном следе Р₁ плоскости Р (рис. 31), а фронтальная проекция К₂ точки пересечения прямой АВ с фронтально проецирующей плоскостью Q (рис. 32) расположена на фронтальном следе Q₂. В этом случае точку пересечения прямой с плоскостью определяем по ее фронтальной проекции.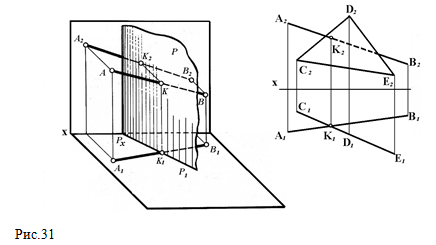

Чтобы построить точку пересечения прямой с профильно проецирующей плоскостью, надо отметить сначала профильную проекцию искомой точки, которая будет принадлежать профильному следу заданной профильно проецирующей плоскости.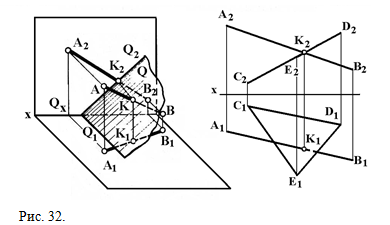

Если прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости на основании теоремы о проецировании прямого угла. При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.

ЗАПОМНИТЕ! Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость также в прямой угол (теорема о проецировании прямого угла).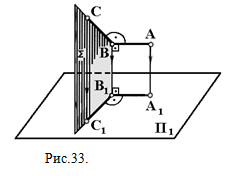

Рассмотрим доказательство теоремы. Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости П₁ (рис.33). Проецирующая плоскость Σ перпендикулярна плоскости П₁ . Значит, АВ _|_ Σ, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В₁С₁. Но, так как АВ || А₁В₁ _|_В₁С₁, т. е. на плоскости П₁ угол между А₁В₁ и В₁С₁ равен 90°.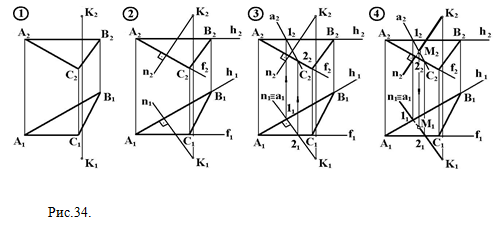

На рис. 34 (1-4) построены проекции основания М перпендикуляра п, проведенного к плоскости треугольника ABC из точки К пространства. В треугольнике AВС имеем: АВ — горизонталь (A₂B₂ _|_ A₂A₁), AC — фронталь (А₁С₁ _|_A₁A₂). Поэтому проекции перпендикуляра n проходят через точку К и располагаются: п₁ _|_A₁B₁ и n₂ _|_ А₂С₂. Основание перпендикуляра на плоскости построено с помощью вспомогательной линии а, которая принадлежит плоскости, лежащей в одной с перпендикуляром п горизонтально проецирующей плоскости. Тогда при пересечении прямых а и п, мы получим точку М- основание перпендикуляра к плоскости .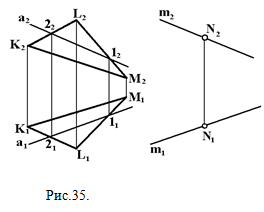

Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 35 построена прямая т, проходящая через точку N и параллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что m₁ || а₁ и m₂ || а₂, а прямая a KLM.