Прямая и точка в плоскости

Прямая линия может принадлежать и не принадлежать плоскости. Если прямая не принадлежит плоскости, она может располагаться параллельно этой плоскости или пересекать ее.

Прямая линия принадлежит плоскости, если она проходит:

1) через две точки, принадлежащие данной плоскости;

Схема

2) через одну точку, принадлежащую плоскости, и параллельна какой-либо прямой, лежащей в данной плоскости или плоскости, ей параллельной. На рис. 21 показана плоскость, которая задана двумя пересекающимися прямыми a и b. Прямая l принадлежит данной плоскости, так как ее точки 1 и 2 принадлежат этой плоскости. Прямая параллельна плоскости, если она параллельна другой прямой, лежащей в этой плоскости. На рис. 21 прямая m параллельна заданной плоскости, так как она параллельна прямой l, принадлежащей этой плоскости.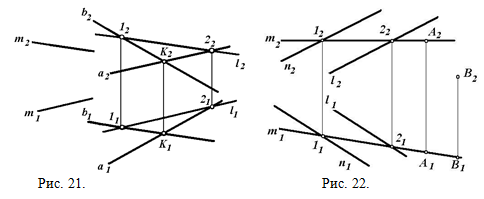

Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей. Эти случаи будут рассмотрены в § 6.

Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости. На рис. 22 показан комплексный чертеж плоскости, заданной двумя параллельными прямыми l и п. В плоскости расположена линия m. Точка A лежит в заданной плоскости, так как она лежит на прямой m. Точка В не принадлежит плоскости, так как ее вторая проекция не лежит на соответствующей проекции прямой m.

ЗАПОМНИТЕ!

1. Принадлежность прямой плоскости определяется принадлежностью двух ее точек данной плоскости, или принадлежностью одной точки этой прямой плоскости и параллельностью этой прямой какой-либо прямой плоскости.

2. Признаком принадлежности точки и прямой плоскости частного положения является совмещение на чертеже их проекций с одноименными следами-проекциями данной плоскости.

Задача 1. Задана плоскость АВС и горизонтальная проекция a₁ прямой a , которая принадлежит плоскости АВС (a ∈ ABC). Построить эпюр плоскости и прямой (рис.23).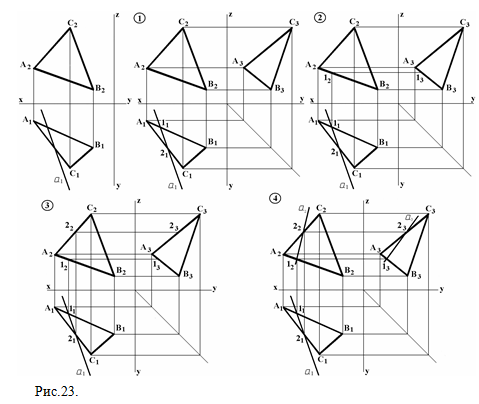

1) построим эпюр плоскости АВС и отметим точки пересечения проекции a₁ c прямыми А₁В₁ – точка l₁ и А₁С₁ – точка 2₁;

2) l₁ из точки l₂ проведем линию связи (⊥оси ОХ) до пересечения с А₂В₂, отметим 1₂; из точки 1₂ проведем линию связи ( оси О ) до пересечения с А₃В₃, отметим 1₃;

3) из точки 2₁ проведем линию связи ( ⊥оси ОХ) до пересечения с А₂С₂, отметим 2₂; из точки 2₂ проведем линию связи ( оси О ) до пересечения с А₃С₃, отметим 2₃;

4) через точки 1₂ и 2₂ проведем прямую a₂ – фронтальную проекцию прямой a ; через точки 1₃ и 2₃ проведем прямую a₃ - профильную проекцию прямой a .

Задача 2. Задана плоскость АВС (А₁В₁С₁; А₂В₂С₂) и прямая b ( b₁;b₂ ).

Определить принадлежит ли прямая b плоскости ABC(b∈ABC) (рис.24).

1) отметим 1₁ и 2₁ – точки пересечения прямой b₁с отрезками А₁С₁ и С₁В₁;

2) из 1₁ и 2₁ проведем линии связи (⊥оси Х) до пересечения с и отметим точки 1₂ и 2₂;

3) точка 2 принадлежит прямой b и плоскости АВС; точка 1 принадлежит прямой b , но не принадлежит плоскости АВС. Следовательно, прямая b не принадлежит плоскости АВС.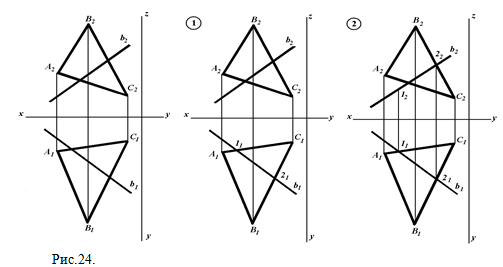

ЗАПОМНИТЕ! Точка принадлежит плоскости, если она расположена на прямой, которая принадлежит этой плоскости.

Задача 3. Задана плоскость АВС (А₂В₂С₂; А₃В₃С₃) и D₂ - фронтальная проекция точки D , (D∈ABC ). Построить эпюр и изометрию плоскости АВС и точки D (рис.25).

1) построим эпюр плоскости АВС; через D₂ и любую точку треугольника А₂В₂С₂, например В₂, проведем прямую и отметим 1₂ – точку пересечения этой прямой с отрезком А₂С₂;

2) через 1₂ проведем линию связи (⊥оси Х) до пересечения с отрезком А₁С₁ и отметим 1₁;;

3) соединим В₁ и 1₁; из D₁ проведем линию связи до пересечения с В₁1₁, отметим D₁ ;

4) из D ₂ и D₁ проведем линии связи до их пересечения, отметим D ₃ ;

5) построим изометрию плоскости АВС и точки D .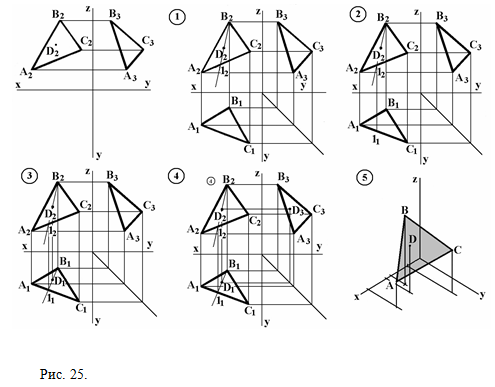

Задача 4. Задана плоскость АВС (А₁В₁С₁; А₃В₃С₃) и N₃ - профильная проекция точки N,N∈ABC . Постройте эпюр и изометрию плоскости АВС и точки N (рис.26).

1) построим эпюр плоскости АВС; из N₃; проведем линию связи до пересечения с отрезком А₁С₁, отметим N₁;

2) из N₃ и N₁ проведем линии связи до их пересечения, отметим N;

3) построим изометрию плоскости АВС и точки N .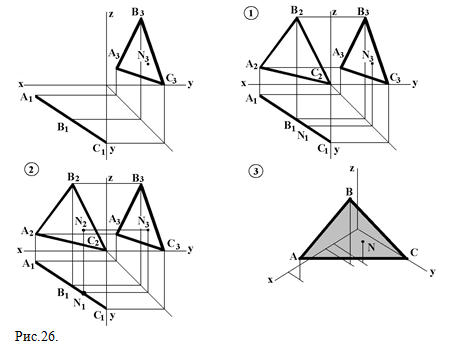