

|
Определение истинной величины расстояний и углов Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проецирующей плоскости есть линия уровня, то необходимо преобразовать чертеж. Заданная плоскость должна занять положение проецирующей плоскости. На рис. 47 построены проекции перпендикуляра МК, отрезок которого определяет расстояние от точки М до плоскости Q (ABC): 1) систему плоскостей П1/П2 заменяем на систему плоскостей П1/П4 так, что П4_|_Q, а следовательно П1 /П4 _|_ h и h будет проецироваться на плоскость П4 в точку и совпадать с A4 и 14 (A4 ≡ h 4 ≡ 14); 2) из М4 опускаем перпендикуляр на плоскость заданного треугольника и так как М4K4 _|_Q4 , М4K4 - истинная величина расстояний от точки М до плоскости Q; 3) определяем положение горизонтальной проекции точки К из условия, что M1K1_|_K4K1 или || П1/ П4; 4) фронтальная проекция точки K2 построена с помощью высоты точки К, измеренной на плоскости П4. 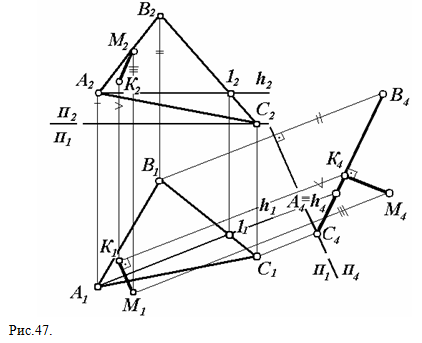
Другой способ решения задачи заключается в следующем (рис.48): плоскость треугольника DEK и точка В вращением вокруг оси, перпендикулярной одной из плоскостей проекций, преобразуются в положение, когда плоскость становится перпендикулярной к одной из плоскостей проекций. В этом случае искомое расстояние измеряется длиной отрезка между новой проекцией точки В и новой проекцией плоскости треугольника DEK. Ось вращения рекомендуется брать проходящей через одну из вершин плоской фигуры (в треугольнике DEK через точку Е). 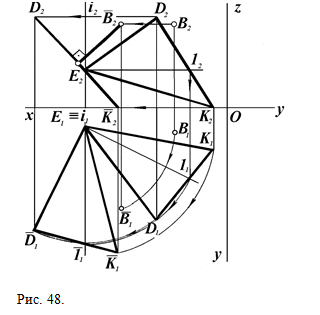
Определить расстояние от точки до плоскости можно и другим способом. Например, через точку В (рис. 49) проводится прямая а перпендикулярно плоскости треугольника DEK , так что а1_|_ h1 и а2_|_ f3 , где h и f - прямые уровня этой плоскости: горизонталь h, фронталь f. Затем находится точка пересечения (встречи) прямой а и плоскости треугольника DEK – точка S. После чего надо определить натуральную величину отрезка ВS (любым известным способом), которая и является искомым расстоянием. 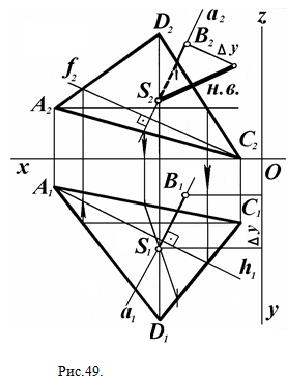
Расстояние от прямой до плоскости, параллельной прямой, измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, затем взять на заданной прямой точку, и решение задачи будет сведено к определению расстояния от точки до плоскости. Расстояние между параллельными плоскостями измеряется отрезком перпендикуляра между ними, который легко строится, если плоскости займут проецирующее положение в новой системе плоскостей проекций. Угол α между прямой l и плоскостью Ω может быть определен через дополнительный угол β между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 50). Угол β дополняет искомый угол α до 90°. Определив истинную величину угла β путем Рис. 50. вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром n, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла α между прямой l и плоскостью Ω. Истинная величина двугранного угла между двумя плоскостями может быть определена, когда ребро угла будет занимать положение проецирующей прямой. На рис.51 задача решена путем замены плоскости проекций с целью преобразования ребра двугранного угла АВ в проецирующую прямую. 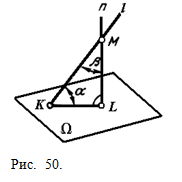
Если ребро двугранного угла не задано, то угол между двумя плоскостями можно определить как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям из произвольной точки М пространства (рис. 52). В плоскости этих перпендикуляров при точке М получаем два плоских угла α и β , которые соответственно равны линейным углам двух смежных углов Рис. 52 (двугранных), образованных плоскостями Р и Q. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями Р и Q. Истинная величина двугранного угла между двумя плоскостями может быть определена, когда ребро угла будет занимать положение проецирующей прямой. На рис.51 задача решена путем замены плоскости проекций с целью преобразования ребра двугранного угла АВ в проецирующую прямую. 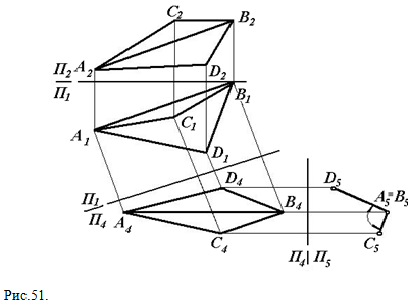
Если ребро двугранного угла не задано, то угол между двумя плоскостями можно определить как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям из произвольной точки М пространства (рис. 52). В плоскости этих перпендикуляров при точке М получаем два плоских угла и , которые соответственно равны линейным углам двух смежных углов 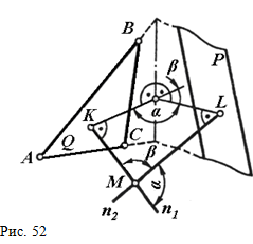 Рис. 52 Рис. 52
(двугранных), образованных плоскостями Р и Q. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями Р и Q. |
