Задание плоскости на чертеже

Из геометрии известно, что через три точки, которые не лежат на одной прямой, можно провести плоскость и только одну, поэтому плоскость в пространстве может быть задана тремя точками, не лежащими на одной прямой.

ЗАПОМНИТЕ! Положение плоскости в пространстве определяют три точки, которые не лежат на одной прямой (рис.1, а).

Плоскость также может быть задана: прямой и точкой, которая не лежит на этой прямой (рис.1, б), двумя пересекающими прямыми (рис.1, в) и двумя параллельными прямыми (рис.2, г), любой плоской фигурой, например, треугольником (ABC) (рис. 1, д). При этом каждый из названных способов задания плоскости допускает возможность перехода от одного из них к другому.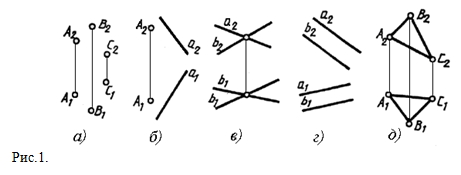

Часть плоскости, которая ограничена линиями, называется плоской фигурой, например: треугольник, квадрат, пятиугольник, круг и другие.

На эпюре плоскость будем задавать проекциями трех точек (рис.2, а), а также проекциями плоской фигуры, то есть проекциями линий, которые ограничивают плоскую фигуру, например, стороны прямоугольника (рис.2, б).

Если плоскость задана тремя точками, то, соединив эти точки, мы получим треугольник. В этом случае говорят, что плоскость задана треугольником (рис.3, а). Чтобы построить третью проекцию такой плоскости, надо построить третью проекцию каждой точки (рис.3, б) и затем соединить их (рис.3, в).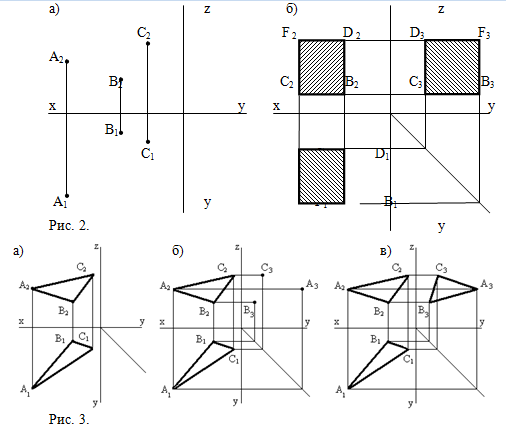

Чтобы построить изометрию плоскости по ее ортогональным проекциям, надо построить изометрию каждой точки, то есть построить координатную ломаную для каждой точки (рис.4, а), и затем соединить их (рис.4, б).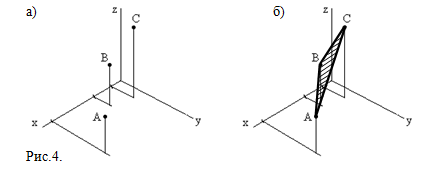

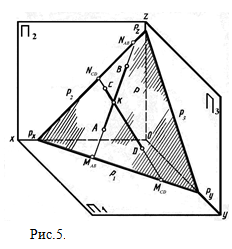
В начертательной геометрии положение плоскости в пространстве может быть определено ее следами, линиями, по которым данная плоскость пересекается с плоскостями проекций.

В общем случае плоскость имеет три следа: горизонтальный — пересечение плоскости с горизонтальной плоскостью проекций П₁, фронтальный и профильный. На рис. 5 они обозначены соответственно Р₁, Р ₂ и Р₃ (буквой Р обозначена заданная плоскость). В точках P_x , P_y , Р_z , лежащих на осях координат, следы плоскости пересекаются между собой. Эти точки называют точками схода следов плоскости.

Следы плоскости всегда можно построить, если положение плоскости в пространстве задано одним из перечисленных выше способов. Проведем по плоскости прямую АВ (рис. 5) и найдем горизонтальный след этой прямой. С этой целью продолжим ее вниз до пересечения с плоскостью П₁. Это случится в точке M_AB, расположенной на линии Р₁, так как по этой линии пересекаются плоскости P и П₁, а прямая АВ принадлежит плоскости Р. Таким образом, горизонтальный след прямой, принадлежащей плоскости, будет расположен на горизонтальном следе плоскости.

Фронтальный след прямой АВ будет точке NAB, расположенной на P2, — фронтальном следе плоскости Р. На соответствующих следах плоскости будут расположены горизонтальный и фронтальный следы любой другой прямой, принадлежащей плоскости Р, например прямой СD (рис. 5).

Отсюда следует, что следы плоскости должны проходить через следы прямых, лежащих в плоскости. Чтобы построить след плоскости, обходимо определить следы двух прямых, принадлежащих плоскости.

Пусть плоскость будет задана двумя пересекающимися прямыми АВ и СD (рис. 6). Чтобы построить горизонтальный след плоскости Р₁, находим горизонтальные следы прямой АВ — точку М_AB и прямой CD — точку M_CD. Горизонтальный след Р₁ плоскости Р будет проходить через точки М_AB и М_CD. Фронтальный след плоскости Р₂ строится аналогично. Следует отметить, что в данном случае для построения следа Р₂ достаточно иметь фронтальный след только одной прямой CD или АВ - точку N_AB или CD — точку N_CD, так как второй точкой, определяющей положение следа Р₂, будет точка схода следов Р_x (точка пересечения ранее построенного следа Р_i с осью х).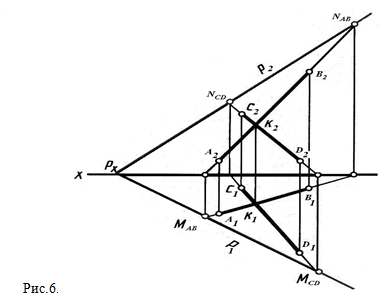

Различают частные и общие случаи расположения плоскости в пространстве относительно плоскостей проекций.